题目内容
在梯形ABCD中，点E、F分别在腰AB、CD上，EF∥AD，AE∶EB＝m∶n.求证：(m＋n)EF＝mBC＋nAD.
你能由此推导出梯形的中位线公式吗？
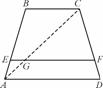
解：如图，连结AC，交EF于点G.
∵ AD∥EF∥BC，
∴ 
＝
＝
，
∴ 
＝
，
＝
.
又EG∥BC，FG∥AD，
∴ ＝
＝，＝
＝，
∴ EG＝·BC，GF＝·AD.
又EF＝EG＋GF，∴ (m＋n)EF＝mBC＋nAD.
∴ 当m＝n＝1时，EF＝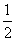
(BC＋AD)，即表示梯形的中位线．
练习册系列答案
小题狂做系列答案
相关题目
；
.
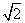sin
，以极点为坐标原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的方程为y＝2x＋1，判断直线l和圆C的位置关系．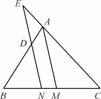
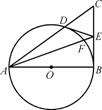
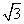，求圆O的半径长和∠EFD的大小．
