题目内容
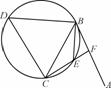
如图，在△ABC中，∠B＝90°，以AB为直径的圆O交AC于D，过点D作圆O的切线交BC于E，AE交圆O于点F.求证：
(1) E是BC的中点；
(2) AD·AC＝AE·AF.
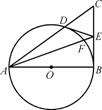
证明：(1) 连结BD，因为AB为圆O的直径，所以BD⊥AC.又∠B＝90°，所以CB切圆O于点B且ED切圆O于点D，因此EB＝ED，所以∠EBD＝∠EDB，∠CDE＋∠EDB＝90°＝∠EBD＋∠C，所以∠CDE＝∠C，得ED＝EC，因此EB＝EC，即E是BC的中点．
(2) 连结BF，显然BF是Rt△ABE斜边上的高，可得△ABE∽△AFB，于是有
＝
，
即AB2＝AE·AF，同理可得AB2＝AD·AC，
所以AD·AC＝AE·AF.
练习册系列答案
相关题目
，其中a∈R，若点P(1，－2)在矩阵M的变换下得到点P′(－4，0)，求实数a的值；并求矩阵M的特征值及其对应的特征向量．
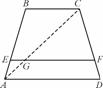
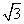，延长CE交AB于点F，求△BCF外接圆的半径．