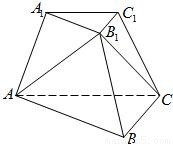
题目内容
已知三棱台ABC-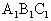 的侧面
的侧面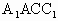 是底角为
是底角为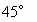 的等腰梯形,且该侧面与底面垂直,∠ACB=
的等腰梯形,且该侧面与底面垂直,∠ACB=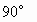 .(1)求证二面角A-
.(1)求证二面角A- -C为直二面角;(2)若AB=5,BC=3,求二面角
-C为直二面角;(2)若AB=5,BC=3,求二面角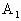 -AB-C的大小.
-AB-C的大小.

答案:
解析:
解析:
|
证(1)延长棱台侧棱相交于点P,过P作PD⊥AC于D,∵面PAC⊥底面ABC,∴PD⊥底面ABC,根据三垂线定理有 (2)过D作DE⊥AB于E,连PE,则PE⊥AB,∴∠PED为二面角 考察所求结论,显然所证结论与上底面 |

练习册系列答案
相关题目
 平面PBA⊥平面PBC.
平面PBA⊥平面PBC. -AB-C的平面角,记作α,依题意易得PD=2,DE=
-AB-C的平面角,记作α,依题意易得PD=2,DE= ,∴tanα=
,∴tanα= ,∴α=arctan
,∴α=arctan 的位置无关.即
的位置无关.即 的位置可处于“游动”状态,因而不妨使它退化为一点P.
的位置可处于“游动”状态,因而不妨使它退化为一点P.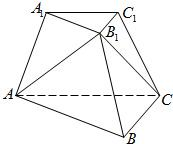 如图,已知三棱台ABC-A1B1C1,等边三角形AB1C所在的平面与底面ABC垂直,且∠ACB=90°,设AC=2a,BC=a.
如图,已知三棱台ABC-A1B1C1,等边三角形AB1C所在的平面与底面ABC垂直,且∠ACB=90°,设AC=2a,BC=a.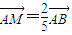 ,|MA1|=x,|CC1|=y,试将y表示为x的函数.
,|MA1|=x,|CC1|=y,试将y表示为x的函数.