题目内容
1.在△ABC中,若a=$\frac{\sqrt{5}}{2}$b,A=2B,则cosB等于( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{\sqrt{5}}{4}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{6}$ |
分析 由题意可得sinA=$\frac{\sqrt{5}}{2}$sinB,sinA=2sinBcosB,联立解方程组可得.
解答 解:∵在△ABC中a=$\frac{\sqrt{5}}{2}$b,∴由正弦定理可得sinA=$\frac{\sqrt{5}}{2}$sinB,①
又∵A=2B,∴sinA=sin2B=2sinBcosB,②
由①②可得$\frac{\sqrt{5}}{2}$sinB=2sinBcosB,
约掉sinB可得cosB=$\frac{\sqrt{5}}{4}$,
故选:B.
点评 本题考查正弦定理解三角形,涉及三角函数公式和解方程组,属基础题.

练习册系列答案
相关题目
13.执行如图的程序框图,如果输入的N=100,则输出的x=( )
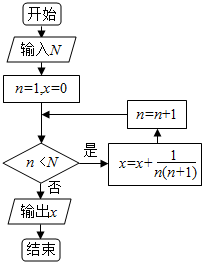

| A. | 0.95 | B. | 0.98 | C. | 0.99 | D. | 1.00 |
10.设α,β∈[0,π],且满足sinαcosβ-cosαsinβ=1,则sin(2α-β)+sin(α-2β)的取值范围为( )
| A. | [-$\sqrt{2}$,1] | B. | [-1,$\sqrt{2}$] | C. | [-1,1] | D. | [1,$\sqrt{2}$] |
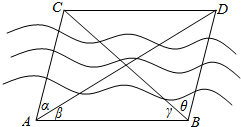 如图,为测不可到达的河北岸C,D两点间的距离,在河南岸选取A,B两点,测得AB=100m,α=β=30°,γ=45°,θ=75°,试求C,D间的距离.
如图,为测不可到达的河北岸C,D两点间的距离,在河南岸选取A,B两点,测得AB=100m,α=β=30°,γ=45°,θ=75°,试求C,D间的距离.