题目内容
8.已知关于x的方程${log_2}({x^2}-2x+5)-|{2a-1}|=0$在x∈[0,3]上有解.(Ⅰ)求正实数a取值所组成的集合A;
(Ⅱ)若t2-at-3≥0对任意a∈A恒成立,求实数t的取值范围.
分析 (Ⅰ)求出${log_2}({x^2}-2x+5)={log_2}[{{{(x-1)}^2}+4}]∈[{2,3}]$,然后推出2≤|2a-1|≤3求解即可.
(Ⅱ)设g(a)=t•a+t2-3,利用恒成立列出不等式组,求解即可.
解答 解:(Ⅰ)当x∈[0,3]时${log_2}({x^2}-2x+5)={log_2}[{{{(x-1)}^2}+4}]∈[{2,3}]$,
2≤|2a-1|≤3且$a>0⇒\frac{3}{2}≤a≤2$,
∴$A=\left\{{a|\frac{3}{2}≤a≤2}\right\}$.
(Ⅱ)由(Ⅰ)知:$\frac{3}{2}≤a≤2$,
设g(a)=t•a+t2-3,
则$\left\{{\begin{array}{l}{g(\frac{3}{2})≥0}\\{g(2)≥9}\end{array}}\right.⇒\left\{{\begin{array}{l}{t≥\frac{{\sqrt{57}-3}}{4}}\\{t≥1或t≤-3}\end{array}}\right.$,$\left\{\begin{array}{l}{g(\frac{3}{2})≥0}\\{g(2)≥0}\end{array}\right.$⇒$\left\{\begin{array}{l}{t\frac{\sqrt{57}-3}{4}或t≤\frac{-\sqrt{57}-3}{4}}\\{t≤-3或t≥1}\end{array}\right.$.
可得$t≥\frac{\sqrt{57}-3}{4}$或t≤-3.
点评 本题考查函数的零点判定定理的应用,函数恒成立,考查转化思想以及计算能力.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
17.圆C与x轴相切于T(1,0),与y轴正半轴交于两点A、B,且|AB|=2,则圆C的标准方程为( )
| A. | (x-1)2+(y-$\sqrt{2}$)2=2 | B. | (x-1)2+(y-2)2=2 | C. | (x+1)2+(y+$\sqrt{2}$)2=4 | D. | (x-1)2+(y-$\sqrt{2}$)2=4 |
19.设方程5-x=|lgx|的两个根分别为x1,x2,则( )
| A. | x1x2<0 | B. | x1x2=1 | C. | x1x2>1 | D. | 0<x1x2<1 |
 为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:[20,25),[25,30),[30,35),[35,40),[40,45],并得到如下频率分布直方图.
为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:[20,25),[25,30),[30,35),[35,40),[40,45],并得到如下频率分布直方图.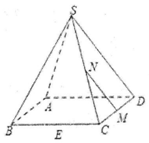 如图,在正四棱锥S-ABCD中,E.M.N分别是BC.CD.SC的中点,动点P的线段MN上运动时,下列四个结论:
如图,在正四棱锥S-ABCD中,E.M.N分别是BC.CD.SC的中点,动点P的线段MN上运动时,下列四个结论: