题目内容
1．已知函数f（x）=xex+ex（e为自然对数的底）（1）求曲线y=f（x）在点（1，f（1））处的切线方程
（2）求y=f（x）的极小值点．
分析 （1）求出函数的导数，计算f（1），f′（1），求出切线方程即可；（2）解关于导函数的不等式，求出函数的单调区间，从而求出函数的极值点即可．
解答 解：（1）∵f（x）=xex+ex，
∴f′（x）=（x+2）ex，
而f（1）=2e，f′（1）=3e，
故切线方程是：y-2e=3e（x-1），
整理得：3ex-y-e=0；
（2）由（1）令f′（x）＞0，解得：x＞-2，
令f′（x）＜0，解得：x＜-2，
故f（x）在（-∞，-2）递减，在（-2，+∞）递增，
故x=-2是函数的极小值点．
点评 本题考查了切线方程问题，考查函数的单调性、极值问题，考查导数的应用，是一道中档题．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
11．设各项均为正的等比数列{an}满足a4a8=3a7，则log3（a1a2…a9）等于（ ）
| A． | 38 | B． | 39 | C． | 9 | D． | 7 |
9．设函数$f（x）=\frac{{{e^2}{x^2}+1}}{x}，g（x）=\frac{{{e^2}x}}{e^x}$，对任意x1，x2∈（0，+∞），不等式$\frac{{g（{x_1}）}}{k}≤\frac{{f（{x_2}）}}{k+1}$恒成立，则正数k的取值范围是（ ）
| A． | [1，+∞） | B． | （1，+∞） | C． | $[\frac{1}{2e-1}，+∞）$ | D． | $（\frac{1}{2e-1}，+∞）$ |
16．函数y=xlnx的最小值为（ ）
| A． | -e-1 | B． | -e | C． | e2 | D． | -$\frac{10}{3}$ |
2．设函数f（x）=x2+bx+c（b，c∈R），若对任意x1，x2∈[-1，1]，有|f（x1）-f（x2）|≤4，则b的取值范围是（ ）
| A． | [0，2] | B． | （0，2] | C． | （-2，2） | D． | [-2，2] |
6．已知点 A（-4，0），B（4，0），C（0，4），直线y=ax+b（a＞0）将△ABC分割为面积相等的两部分，则 b的取值范围是（ ）
| A． | $（{0，4-2\sqrt{2}}）$ | B． | $（{4-2\sqrt{2}，2}）$ | C． | $（{4-2\sqrt{2}，\frac{4}{3}}]$ | D． | $（{\frac{4}{3}，2}]$ |
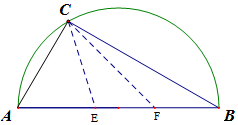如图，有一直径为8米的半圆形空地，现计划种植果树，但需要有辅助光照．半圆周上的C处恰有一可旋转光源满足果树生长的需要，该光源照射范围是$∠ECF=\frac{π}{6}$，点E，F在直径AB上，且$∠ABC=\frac{π}{6}$．