题目内容
已知集合E={x|1-m≤x≤1+m}，F={x|x＜-2或x＞0}，若E∩F=∅，求实数m的取值范围．
考点：集合关系中的参数取值问题
专题：计算题,集合
分析：根据集合E={x|1-m≤x≤1+m}，F={x|x＜-2或x＞0}，E∩F=∅，可得
，解不等式，即可求实数m的取值范围．
|
解答：
解：∵集合E={x|1-m≤x≤1+m}，F={x|x＜-2或x＞0}，E∩F=∅，
∴
，且1-m≤1+m，
∴m=∅．
1-m＞1+m时，m＜0，E是∅，也成立．
∴
|
∴m=∅．
1-m＞1+m时，m＜0，E是∅，也成立．
点评：本题考查的知识点是集合关系中的参数取值问题，考查解不等式，属于基础题．
练习册系列答案
相关题目
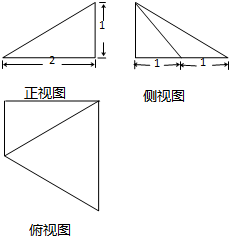某几何体的三视图如图所示，其中正（主）视图与侧（左）视图的边界均为直角三角形，俯视图的边界为直角梯形，则该几何体的体积是（ ）