题目内容
 如图.已知几何体的三视图(单位:cm).
如图.已知几何体的三视图(单位:cm).(Ⅰ)画出它的大致直观图(不要求写画法);
(Ⅱ)求这个几何体的表面积和体积.(结果用π保留)
分析:由三视图可以知道,此几何体是一个底部为圆柱,上部为圆锥的组合体.利用面积公式与体积公式求值即可.
解答: 解(Ⅰ)这个几何体的直观图如图所示.
解(Ⅰ)这个几何体的直观图如图所示.
(Ⅱ)这个几何体是一个简单组合体,它的下部是一个圆柱(底面半径为1cm,高为2cm),它的上部是一个圆锥(底面半径为1cm,母线长为2cm,高为
cm).
所以所求表面积S=π×12+2π×1×2+π×1×2=7π(cm2),
所求体积V=π×12×2+
×π×12×
=2π+
π(cm3).
 解(Ⅰ)这个几何体的直观图如图所示.
解(Ⅰ)这个几何体的直观图如图所示.(Ⅱ)这个几何体是一个简单组合体,它的下部是一个圆柱(底面半径为1cm,高为2cm),它的上部是一个圆锥(底面半径为1cm,母线长为2cm,高为
| 3 |
所以所求表面积S=π×12+2π×1×2+π×1×2=7π(cm2),
所求体积V=π×12×2+
| 1 |
| 3 |
| 3 |
| ||
| 3 |
点评:本题考点是由三视图求面积与体积,本题主要考查根据三视图的作图规则还原实物图的能力,三视图的作图规则是主视图与俯视图长对正,主视图与侧视图高平齐,侧视图与俯视图是宽相等,本题是考查利用三视图的作图规则把三视图中的数据还原到原始图形中来,求面积与体积,做题时要注意正确利用三视图中所提供的信息,正确地得出实物图的长宽高等数据.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
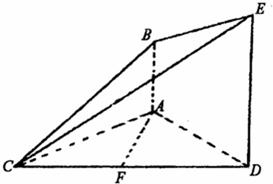 如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB=2,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB=2,且F是CD的中点. 如图,已知图中的三个直角三角形是一个几何体的三视图,那么这个几何体的体积等于
如图,已知图中的三个直角三角形是一个几何体的三视图,那么这个几何体的体积等于 如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求:
如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求: 如图,已知三棱锥P-ABC的侧面PAC是底角为45°的等腰三角形,PA=PC,且该侧面垂直于底面,∠ACB=90°,AB=10,BC=6,B1C1=3.
如图,已知三棱锥P-ABC的侧面PAC是底角为45°的等腰三角形,PA=PC,且该侧面垂直于底面,∠ACB=90°,AB=10,BC=6,B1C1=3.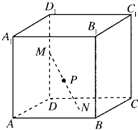 如图,已知正方体ABCD-A1B1C1D1的棱长为a(a>2),长度为2的线段MN的一个端点M在DD1上运动,另一端点N在底面ABCD上运动,则MN的中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体的体积为
如图,已知正方体ABCD-A1B1C1D1的棱长为a(a>2),长度为2的线段MN的一个端点M在DD1上运动,另一端点N在底面ABCD上运动,则MN的中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体的体积为