Question

【题目】如图，在边长为2的正六边形ABCDEF中，动圆Q的半径为1，圆心在线段CD（含端点）上运动，P是圆Q上及内部的动点，设向量 （m，n为实数），则m+n的取值范围是（　　）

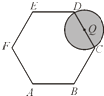
A.（1，2]
B.[5，6]
C.[2，5]
D.[3，5]

Answer 1

【答案】C
【解析】解：如图所示，

①设点O为正六边形的中心，则 ．

当动圆Q的圆心经过点C时，与边BC交于点P，点P为边BC的中点．连接OP，

则 ，

∵ 与 共线，∴存在实数t，使得 ．

∴ = + = = ，

此时m+n=1+t+1﹣t=2，取得最小值．

②当动圆Q的圆心经过点D时，取AD的延长线与⊙Q的交点P时．

= = ，

此时m+n= =5取得最大值．

因此m+n的取值范围是[2，5]．

所以答案是：C．