题目内容

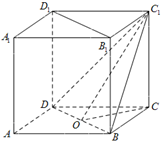
正四棱锥相邻二侧面形成的二面角为θ，则θ的取值范围是（　　）
A．（0，
π
2
）		B．（
π
3
，
π
2
）		C．（
π
4
，
π
3
）		D．（
π
2
，π）
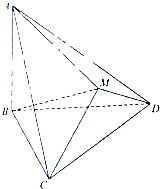
正四棱锥S-ABCD中，设AE、CE垂直于SB，
则∠AEC为二面角A-PB-C的平面角，且AE＜AB，CE＜CB
因为由勾股定理得，AC2=AB2+CB2，
所以AC2＞AE2+CE2，
在△AEC中，由余弦定理得，cos∠AEC=
AE2+CE2-AC2
2AE•CE
＜0
∴∠AEC∈（
π
2
，π）
故选D．
练习册系列答案
相关题目
如图，在长方体ABCD-A1B1C1D1中，AB=BC=2AA1，则BC1与平面BB1D1D所成角的正弦值为______．
已知二面角α-l-β的大小为120°，点B，C在棱l上，A∈α，D∈β，AB⊥l，CD⊥l，AB=2，BC=1，CD=3，则AD的长为______．
如图△BCD与△MCD都是边长为2的正三角形，平面MCD⊥平面BCD，AB⊥平面BCD，AB=2
3
．
（1）求点A到平面MBC的距离；
（2）求平面ACM与平面BCD所成二面角的正弦值．
如图，正方体AC1
（1）在BD上确定一点E，使D1E∥面A1C1B；
（2）求直线BB1和面A1C1B所成角的正弦值；
（3）求面A1C1B与底面ABCD所成二面角的平面角的正弦值．
如图，在棱长为1的正方体ABCD-A1B1C1D1中，P是AC与BD的交点，M是CC1的中点．
（1）求证：A1P⊥平面MBD；
（2）求直线B1M与平面MBD所成角的正弦值；
（3）求平面ABM与平面MBD所成锐角的余弦值．
已知正三棱柱ABC-A1B1C1的每条棱长均为a，M为棱A1C1上的动点．
（1）当M在何处时，BC1∥平面MB1A，并证明之；
（2）在（1）下，求平面MB1A与平面ABC所成的二面角的大小；
（3）求B-AB1M体积的最大值．
正四棱锥的底面积为Q，侧面积为P，侧面与底面所成的二面角为α，则cosα=______．
如图，在棱长为1的正方体ABCD-A1B1C1D1中，点O是BD中点．
（Ⅰ）求证：平面BDD1B1⊥平面C1OC；
（Ⅱ）求二面角C1-BD-C的正切值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网