题目内容
已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.
(1)当M在何处时,BC1∥平面MB1A,并证明之;
(2)在(1)下,求平面MB1A与平面ABC所成的二面角的大小;
(3)求B-AB1M体积的最大值.
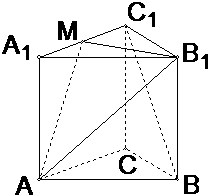
(1)当M在何处时,BC1∥平面MB1A,并证明之;
(2)在(1)下,求平面MB1A与平面ABC所成的二面角的大小;
(3)求B-AB1M体积的最大值.

(I)当M在A1C1中点时,BC1∥平面MB1A
∵M为A1C1中点,延长AM、CC1,使AM与CC1延长线交于N,则NC1=C1C=a
连接NB1并延长与CB延长线交于G,则BG=CB,NB1=B1G(2分)
在△CGN中,BC1为中位BC1∥GN
又GN?平面MAB1,∴BC1∥平面MAB1(4分)
(II)∵△AGC中,BC=BA=BG∴∠GAC=90°
即AC⊥AG又AG⊥AA1AA1∩AC=A∴AG⊥平面A1ACC1,AG⊥AM(6分)
∴∠MAC为平面MB1A与平面ABC所成二面角的平面角∴tan∠MAC=
=2
∴所求二面角为 arctan2.(8分)
(Ⅲ)设动点M到平面A1ABB1的距离为hM.VB-AB1M=VM-AB1B=
S△ABB1•hM=
•
a2hM≤
a2•
a=
a3
即B-AB1M体积最大值为
a3.此时M点与C1重合.(12分)
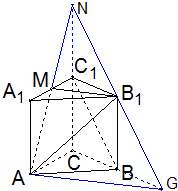
∵M为A1C1中点,延长AM、CC1,使AM与CC1延长线交于N,则NC1=C1C=a
连接NB1并延长与CB延长线交于G,则BG=CB,NB1=B1G(2分)
在△CGN中,BC1为中位BC1∥GN
又GN?平面MAB1,∴BC1∥平面MAB1(4分)
(II)∵△AGC中,BC=BA=BG∴∠GAC=90°
即AC⊥AG又AG⊥AA1AA1∩AC=A∴AG⊥平面A1ACC1,AG⊥AM(6分)
∴∠MAC为平面MB1A与平面ABC所成二面角的平面角∴tan∠MAC=
| a | ||
|
∴所求二面角为 arctan2.(8分)
(Ⅲ)设动点M到平面A1ABB1的距离为hM.VB-AB1M=VM-AB1B=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| ||
| 2 |
| ||
| 12 |
即B-AB1M体积最大值为
| ||
| 12 |


练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目