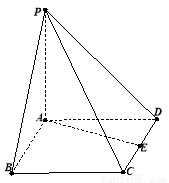题目内容
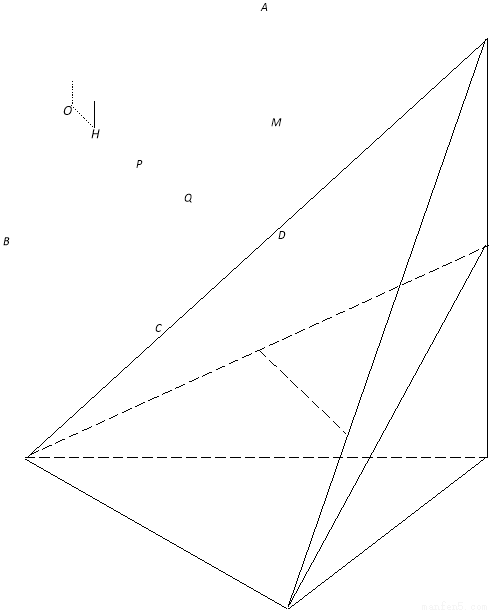
(本小题共14分) 如图,在四面体
如图,在四面体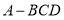 中,
中, 平面
平面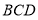 ,
,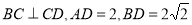 .
.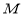 是
是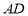 的中点,
的中点,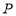 是
是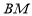 的中点.
的中点.

(Ⅰ)求证:平面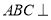 平面
平面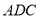 ;
;
(Ⅱ)若点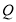 在线段
在线段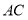 上,且满足
上,且满足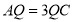 ,求证:
,求证: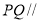 平面
平面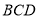 ;
;
(Ⅲ)若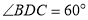 ,求二面角
,求二面角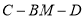 的大小.
的大小.
(Ⅰ)详见解析(Ⅱ)详见解析(Ⅲ)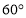
【解析】
试题分析:(Ⅰ)证明面面垂直,一般利用面面垂直判定定理,即从证明线面垂直出发: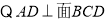
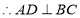 又
又 ,
,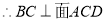
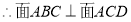 (Ⅱ)证明线面平行,一般利用线面平行判定定理,即从证明线线平行出发,这一般可利用平面几何知识得以证明:取BD中点O则易得四边形
(Ⅱ)证明线面平行,一般利用线面平行判定定理,即从证明线线平行出发,这一般可利用平面几何知识得以证明:取BD中点O则易得四边形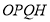 为平行四边形,所以
为平行四边形,所以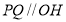 ,所以PQ//面BDC. (Ⅲ)求二面角,一般利用空间向量求解,先建立空间直角坐标系,设点的坐标,求出平面法向量,再利用向量数量积求夹角.
,所以PQ//面BDC. (Ⅲ)求二面角,一般利用空间向量求解,先建立空间直角坐标系,设点的坐标,求出平面法向量,再利用向量数量积求夹角.
试题解析:(Ⅰ)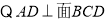 ,
,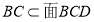
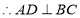 2分
2分
 且
且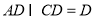
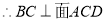
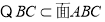
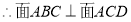 4分
4分
(Ⅱ)证明:如图所示,取BD中点O,且P是BM中点,
所以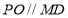 且
且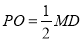 ;
;
取CD的四等分点H,使DH=3CH, 且AQ =3QC,
所以, 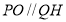 且
且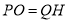 ,
,
所以,四边形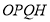 为平行四边形,
为平行四边形,
所以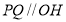 ,且
,且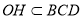 ,
,
所以PQ//面BDC. 9分
(Ⅲ)如图建系,
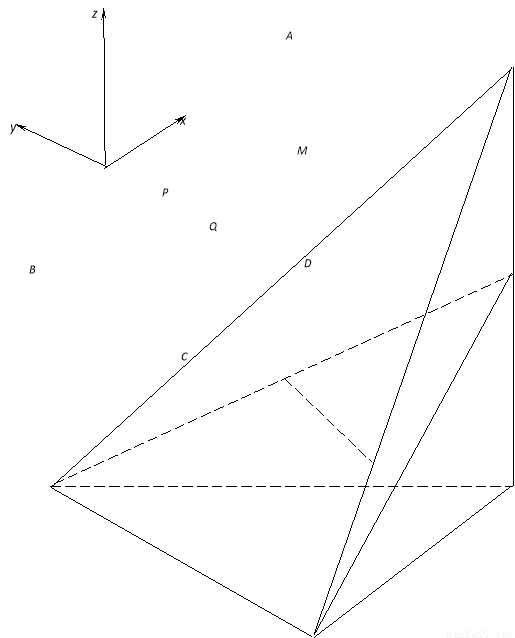
则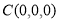 ,
, ,
,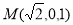 ,
,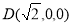 10分
10分
设面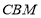 的法向量
的法向量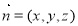
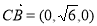 ,
,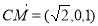
 ,即
,即
令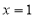 ,则
,则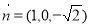
设面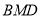 的法向量
的法向量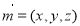 11分
11分
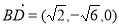
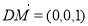
 即
即
令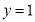 , 则
, 则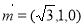 12分
12分
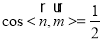
所以二面角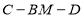 的大小为
的大小为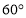 14分
14分
考点:面面垂直判定定理,线面平行判定定理,利用空间向量求二面角

练习册系列答案
相关题目
 ,
,  ,则
,则 .
.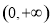 上单调递增,并且是偶函数的是( )
上单调递增,并且是偶函数的是( )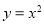 (B)
(B)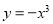 (C)
(C)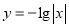 (D)
(D)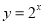
 的焦点与双曲线
的焦点与双曲线 的焦点重合,则
的焦点重合,则 的值为 .
的值为 .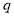 为公比的等比数列
为公比的等比数列 中,
中,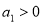 ,则“
,则“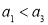 ”是“
”是“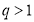 ”的( )
”的( )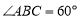 .
.