Question

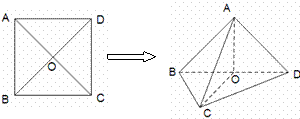
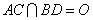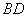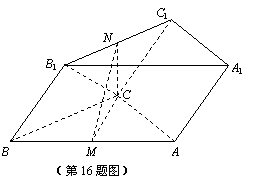
已知正方形ABCD的边长为1，．将正方形ABCD沿对角线折起，使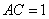，得到三棱锥A—BCD，如图所示．

（I）若点M是棱AB的中点，求证：OM∥平面ACD；

（II）求证：；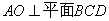

（III）求二面角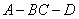的余弦值．

Answer 1

 (I) 在正方形ABCD中，是对角线的交点，

O为BD的中点，  M为AB的中点， OM∥AD.

又AD平面ACD，OM平面ACD， OM∥平面ACD. 

（II）证明：在中，，，

，.

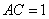又 是正方形ABCD的对角线，，

又.

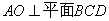（III）由（II）知_，则OC，OA，OD两两互相垂直，如图，以O为原点，建立空间直角坐标系.则，               

是平面的一个法向量.，，                      

设平面的法向量,则，.

即， 

所以且令则，，解得.

从而，二面角的余弦值为.