题目内容
设函数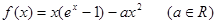 .
.
(1)当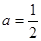 时,求函数
时,求函数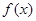 的单调区间;
的单调区间;
(2)若当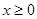 时
时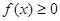 ,求a的取值范围.
,求a的取值范围.
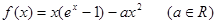 .
.(1)当
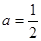 时,求函数
时,求函数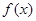 的单调区间;
的单调区间;(2)若当
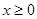 时
时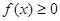 ,求a的取值范围.
,求a的取值范围.(1)增区间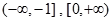 ,减区间
,减区间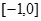 ;(2)
;(2)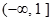
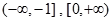 ,减区间
,减区间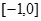 ;(2)
;(2)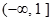
试题分析:(1)由
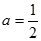 得到
得到 ,求其导数
,求其导数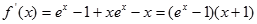 ,解不等式
,解不等式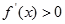 得到函数的增区间, 解不等式
得到函数的增区间, 解不等式 得到函数的减区间;(2)法一:由当
得到函数的减区间;(2)法一:由当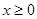 时
时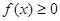 得:
得: 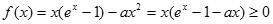 等价于:
等价于: 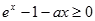 在
在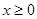 时恒成立,令
时恒成立,令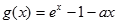 ,注意到
,注意到 ,所以只需
,所以只需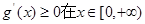 上恒成立即可,故有
上恒成立即可,故有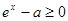 在
在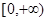 上恒成立,则
上恒成立,则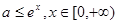 所以有
所以有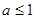 .法二:将
.法二:将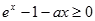 在
在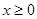 时恒成立等价转化为:
时恒成立等价转化为: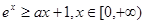 恒成立
恒成立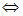 函数
函数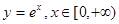 的图象恒在函数
的图象恒在函数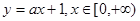 图象的上方,由图象可求得a的取值范围.
图象的上方,由图象可求得a的取值范围.试题解析:(1)当
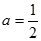 时,
时, ,
,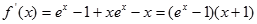
当
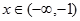 时,
时,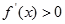 ;当
;当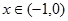 时,
时, 时,
时,当
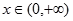 时,
时,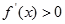 ,
,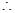 增区间
增区间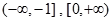 ,减区间
,减区间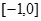
(2)法一:
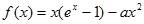 ,令
,令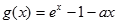 ,则
,则
若
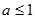 ,则当
,则当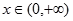 时,
时, 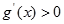 ,
, 为增函数,而
为增函数,而 ,
,从而当
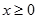 时,
时,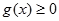 ,即
,即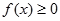
若
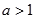 ,则当
,则当 时,
时,
 为减函数,而
为减函数,而 ,从而当
,从而当 时,
时, ,即
,即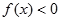
综上得
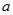 的取值范围为
的取值范围为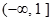 .
.法二: 由当
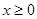 时
时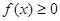 得:
得: 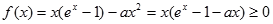 等价于:
等价于: 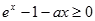 在
在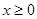 时恒成立,等价转化为:
时恒成立,等价转化为: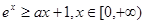 恒成立
恒成立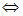 函数
函数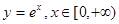 的图象恒在函数
的图象恒在函数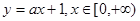 图象的上方,如图:,由于直线
图象的上方,如图:,由于直线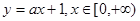 恒过定点,而
恒过定点,而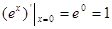 ,所以函数
,所以函数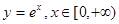 图象在点(0,1)处的切线方程为:
图象在点(0,1)处的切线方程为: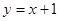 ,故知:
,故知: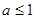 ,即
,即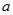 的取值范围为
的取值范围为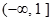 .
.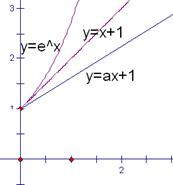

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 ,(
,(  为常数,
为常数, 为自然对数的底).
为自然对数的底). 时,求
时,求 ;
; 在
在 时取得极小值,试确定
时取得极小值,试确定 ,将
,将 ,试判断曲线
,试判断曲线 是否能与直线
是否能与直线 (
( 为确定的常数)相切,并说明理由.
为确定的常数)相切,并说明理由. 是偶函数,
是偶函数, 是它的导函数,当
是它的导函数,当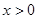 时,
时,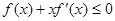 恒成立,且
恒成立,且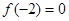 ,则不等式
,则不等式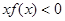 的解集为 。
的解集为 。 ,且对任意实数x,总有
,且对任意实数x,总有 /(x)<3
/(x)<3 <3x-15的解集为( )
<3x-15的解集为( ) x2+4x-3ln x在[t,t+1]上不单调,则t的取值范围是________.
x2+4x-3ln x在[t,t+1]上不单调,则t的取值范围是________.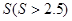 平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米,已知后面墙的造价为每米45元,其它墙的造价为每米180元,设后面墙长度为x米,修建此矩形场地围墙的总费用为
平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米,已知后面墙的造价为每米45元,其它墙的造价为每米180元,设后面墙长度为x米,修建此矩形场地围墙的总费用为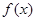 元.
元.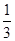 x3+
x3+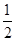 x2+2ax,若f(x)在(
x2+2ax,若f(x)在(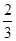 ,+∞)上存在单调递增区间,则实数a的取值范围为( )
,+∞)上存在单调递增区间,则实数a的取值范围为( )