题目内容
设f(x)=-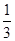 x3+
x3+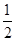 x2+2ax,若f(x)在(
x2+2ax,若f(x)在(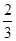 ,+∞)上存在单调递增区间,则实数a的取值范围为( )
,+∞)上存在单调递增区间,则实数a的取值范围为( )
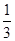 x3+
x3+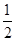 x2+2ax,若f(x)在(
x2+2ax,若f(x)在(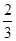 ,+∞)上存在单调递增区间,则实数a的取值范围为( )
,+∞)上存在单调递增区间,则实数a的取值范围为( )A.a>-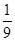 | B.a<-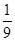 | C.a>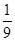 | D.不存在 |
A
f′(x)=-x2+x+2a=-(x-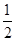 )2+
)2+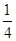 +2a,
+2a,
∵f(x)在(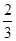 ,+∞)上存在单调递增区间,∴存在(
,+∞)上存在单调递增区间,∴存在(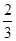 ,+∞)的子区间(m,n),使得x∈(m,n)时,f′(x)>0.
,+∞)的子区间(m,n),使得x∈(m,n)时,f′(x)>0.
∵f′(x)在(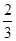 ,+∞)上单调递减,∴f′(
,+∞)上单调递减,∴f′(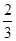 )>0,即f′(
)>0,即f′(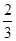 )=
)=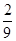 +2a>0,解得a>-
+2a>0,解得a>-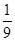 ,∴当a>-
,∴当a>-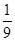 时,f(x)在(
时,f(x)在(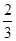 ,+∞)上存在单调递增区间.
,+∞)上存在单调递增区间.
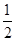 )2+
)2+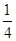 +2a,
+2a,∵f(x)在(
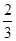 ,+∞)上存在单调递增区间,∴存在(
,+∞)上存在单调递增区间,∴存在(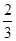 ,+∞)的子区间(m,n),使得x∈(m,n)时,f′(x)>0.
,+∞)的子区间(m,n),使得x∈(m,n)时,f′(x)>0.∵f′(x)在(
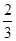 ,+∞)上单调递减,∴f′(
,+∞)上单调递减,∴f′(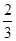 )>0,即f′(
)>0,即f′(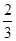 )=
)=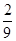 +2a>0,解得a>-
+2a>0,解得a>-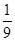 ,∴当a>-
,∴当a>-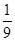 时,f(x)在(
时,f(x)在(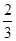 ,+∞)上存在单调递增区间.
,+∞)上存在单调递增区间.
练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
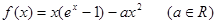 .
.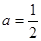 时,求函数
时,求函数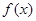 的单调区间;
的单调区间;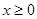 时
时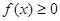 ,求a的取值范围.
,求a的取值范围. ,若
,若 在
在 上的最小值记为
上的最小值记为 .
. 时,恒有
时,恒有 .
. .
. 时,讨论
时,讨论 的单调性;
的单调性; ,当
,当 若对任意
若对任意 存在
存在 使
使 求实数
求实数 的取值范围。
的取值范围。 x2.
x2.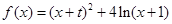 的图象在点
的图象在点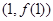 处的切线垂直于
处的切线垂直于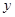 轴.
轴.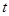 的值;
的值;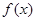 的极值.
的极值.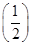 ,c=f(3),则a,b,c的大小关系为____________.
,c=f(3),则a,b,c的大小关系为____________. R,求函数
R,求函数 在区间
在区间 上的最小值.
上的最小值. 在区间
在区间 上是单调递增函数,则实数
上是单调递增函数,则实数 的取值范围是 .
的取值范围是 .