题目内容
1.已知a,b,c分别是△ABC内角A,B,C的对边sin2B=2sinAsinC,a=b(1)求cosA
(2)若a=$\sqrt{2}$,求△ABC的面积.
分析 (1)由sin2B=2sinAsinC,根据正弦定理可得:b2=2ac,a=b,利用余弦定理可求cosA的值.
(2)a=$\sqrt{2}$,根据(1)可得b,c的值和sinA的值,根据${S}_{△ABC}=\frac{1}{2}bcsinA$可得结论.
解答 解:(1)由sin2B=2sinAsinC,根据正弦定理可得:b2=2ac,
又∵a=b,
可得:b=2c
则$cosA=\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{{c}^{2}}{4{c}^{2}}=\frac{1}{4}$.
(2)由(1)知:b=2c,而a=b=$\sqrt{2}$,
根据$cosA=\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{1}{4}$
解得:c=$\frac{\sqrt{2}}{2}$.
∵cosA=$\frac{1}{4}$,则sinA=$\sqrt{1-sinA}=\frac{\sqrt{15}}{4}$,
则${S}_{△ABC}=\frac{1}{2}bcsinA$=$\frac{1}{2}×2\sqrt{2}×\sqrt{2}×\frac{\sqrt{15}}{4}$=$\frac{\sqrt{15}}{2}$.
点评 本题考查三角形的正弦定理和余弦定理的运用,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若直线2x-y+2=0与直线y=kx+1平行,则实数k的值为( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
16.已知集合A={x|$\sqrt{2x-1}$>1},则∁RA=( )
| A. | {x|x>1} | B. | {x|x≥$\frac{1}{2}$} | C. | {x|x≤1} | D. | {x|x<$\frac{1}{2}$} |
6.“-1≤x≤2”是“x2-x-2=0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 冲要条件 | D. | 既不充分也不必要条件 |
9.已知a=0.78,b=80.7,c=log0.78,则a、b、c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>b>a |
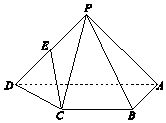 如图,在四棱锥P-ABCD中,AD∥BC,∠BAD=90°,PA=PD,AB⊥PA,AD=2,AB=BC=1
如图,在四棱锥P-ABCD中,AD∥BC,∠BAD=90°,PA=PD,AB⊥PA,AD=2,AB=BC=1