题目内容
已知函数  ,
, .
.
(Ⅰ)当  时,求函数
时,求函数  的最小值;
的最小值;
(Ⅱ)当  时,讨论函数
时,讨论函数  的单调性;
的单调性;
(Ⅲ)求证:当  时,对任意的
时,对任意的  ,且
,且 ,有
,有 .
.
(Ⅰ)显然函数 的定义域为
的定义域为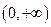 ,
,
当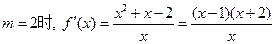 .
.
∴ 当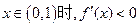 ,
,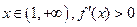 .
.
∴ 在
在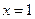 时取得最小值,其最小值为
时取得最小值,其最小值为 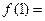
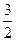 .-- ------- 4分
.-- ------- 4分
(Ⅱ)∵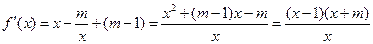 ,-------5分
,-------5分
∴(1)当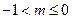 时,若
时,若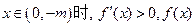 为增函数;
为增函数; 为减函数;
为减函数;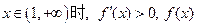 为增函数.
为增函数.
(2)当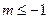 时,
时,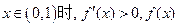 为增函数;
为增函数;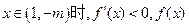 为减函数;
为减函数;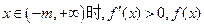 为增函数.----- 9分
为增函数.----- 9分
(Ⅲ)不妨设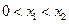 ,要证明
,要证明 ,即证明:
,即证明: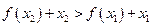
当 时,函数
时,函数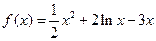 .
.
考查函数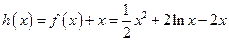 -------------------10分
-------------------10分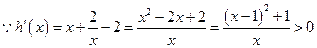
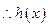 在
在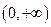 上是增函数,-------------------12分
上是增函数,-------------------12分
对任意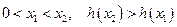 ,
,
所以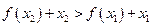 ,
,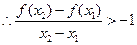 命题得证
命题得证
解析

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
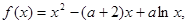
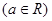
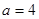 ,方程
,方程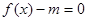 有三个不同的根,求
有三个不同的根,求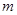 的取值范围。
的取值范围。
 .
.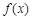 的单调区间;
的单调区间; ,若对任意
,若对任意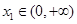 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.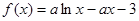 ,
,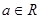
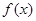 的单调区间。
的单调区间。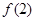 )处的切线的倾斜角为
)处的切线的倾斜角为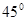 ,对任意的
,对任意的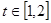 ,函数
,函数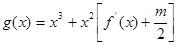 在区间
在区间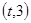 上总不是单调函数,求m取值范围
上总不是单调函数,求m取值范围
 上的函数
上的函数 ,其中
,其中 为大于零的常数.
为大于零的常数. 时,令
时,令 ,
, 时,
时, (
( 为自然对数的底数);
为自然对数的底数); ,在
,在 处取得最大值,
处取得最大值, (
( 为实数).
为实数). 在
在 处有极值,求
处有极值,求 上是增函数,求
上是增函数,求 .
. 在
在 上的最小值;
上的最小值; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. ,
, .
. 的单调区间和最小值;
的单调区间和最小值; 的大小关系;
的大小关系;
 的取值范围,使得
的取值范围,使得 <
< 对任意
对任意 >0成立
>0成立 .
. ,
,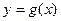 在
在 处的切线相互垂直,求这两个切线方程;
处的切线相互垂直,求这两个切线方程; 单调递增,求
单调递增,求 的取值范围.
的取值范围.