题目内容
9.是否存在实数a,使得函数y=sin2x+acosx在区间$[0,\frac{π}{2}]$上的最大值为1?若存在,求出相对应的a的值;若不存在,请说明理由.分析 令cosx=t,f(t)=-t2+at+1,令f(t)在[0,1]上的最大值为1解出a即可.
解答 解:y=sin2x+acosx=-cos2x+acosx+1,x∈[0,$\frac{π}{2}$],
令cosx=t,则t∈[0,1],
令f(t)=-t2+at+1,
(1)若$\frac{a}{2}$≤0,即a≤0时,f(t)在[0,1]上单调递减,
∴fmax(t)=f(0)=1,符合题意;
(2)若$\frac{a}{2}$≥1,即a≥2时,f(t)在[0,1]上单调递增,
∴fmax(t)=f(1)=a=1,即a=1(舍);
(3)若0<$\frac{a}{2}$<1,即0<a<2时,则f(t)在[0,$\frac{a}{2}$)上单调递增,在($\frac{a}{2}$,1]上单调递减,
∴fmax(x)=f($\frac{a}{2}$)=$\frac{{a}^{2}}{4}$+1=1,方程无解;
综上,a≤0.
点评 本题考查了三角函数恒等变换,二次函数的性质,换元思想的应用,属于中档题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
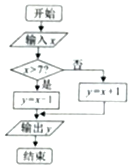 已知实数x的取值范围为[0,10],给出如图所示程序框图,输入一个数x.
已知实数x的取值范围为[0,10],给出如图所示程序框图,输入一个数x.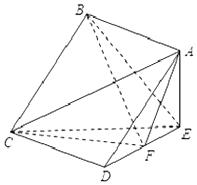 如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.