题目内容
14.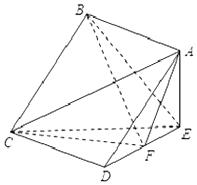 如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.(1)求证:BE∥平面ACF
(2)求异面直线AD与CF所成角的余弦值.
分析 (1)连接AC,BD交于O,连OF,则OF为△DEB的中位线,通过OF∥BE,证明BE∥平面ACF;
(2)异面直线AD与CF所成角就是BC与CF所成角,利用余弦定理可求异面直线AD与CF所成角的余弦值.
解答  (1)证明:连接AC,BD交于O,连OF
(1)证明:连接AC,BD交于O,连OF
∵F为DE中点,O为BD中点,
∴OF∥BE,OF?平面ACF,BE?平面ACF,
∴BE∥平面ACF;
(2)解:∵BC∥AD,
∴异面直线AD与CF所成角就是BC与CF所成角,
∵AE=DE=2,F为线段DE的中点.
∴AD=BC=CD=2$\sqrt{2}$,
∵CF=$\sqrt{8+1}$=3,BF=$\sqrt{8+4+1}$=$\sqrt{13}$,
∴cos∠BCF=$\frac{8+9-13}{2×2\sqrt{2}×3}$=$\frac{\sqrt{2}}{6}$,
∴异面直线AD与CF所成角的余弦值为$\frac{\sqrt{2}}{6}$.
点评 本题考查直线和平面平行关系的判定,直线和平面所成角的计算.考查考查空间想象能力、转化、计算、推理论证能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
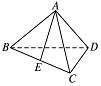
4.如图,空间四边形的各边和对角线长均相等,E 是 BC 的中点,那么( )

| A. | $\overrightarrow{AE}$•$\overrightarrow{BC}$<$\overrightarrow{AE}$•$\overrightarrow{CD}$ | B. | $\overrightarrow{AE}$•$\overrightarrow{BC}$=$\overrightarrow{AE}$•$\overrightarrow{CD}$ | ||
| C. | $\overrightarrow{AE}$•$\overrightarrow{BC}$>$\overrightarrow{AE}$•$\overrightarrow{CD}$ | D. | $\overrightarrow{AE}$•$\overrightarrow{BC}$与 $\overrightarrow{AE}$•$\overrightarrow{CD}$不能比较大小 |
2.A,B,C为△ABC的三个内角,下列关系中不成立的是( )
①cos(A+B)=cosC
②sin(2A+B+C)=sinA
③$cos\frac{B+C}{2}=sin\frac{A}{2}$
④tan(A+B)=-tanC.
①cos(A+B)=cosC
②sin(2A+B+C)=sinA
③$cos\frac{B+C}{2}=sin\frac{A}{2}$
④tan(A+B)=-tanC.
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
3.若$tanθ=\frac{1}{3}$,则sin2θ=( )
| A. | $-\frac{3}{5}$ | B. | $-\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{5}$ |