题目内容
17.函数y=$\frac{4-sinx}{3-cosx}$的最大值为$\frac{{6+\sqrt{6}}}{4}$.分析 函数$y=\frac{4-sinx}{3-cosx}$表示过A(cosx,sinx),B(3,4)的直线的斜率,由直线和圆相切可得.
解答 解:函数$y=\frac{4-sinx}{3-cosx}$表示过A(cosx,sinx),B(3,4)的直线的斜率,
由几何意义可得过定点(3,4)与单位圆相切时的切线斜率为最值,
故设切线的斜率为k,则直线方程为y-4=k(x-3),即kx-y-3k+4=0,
由点到直线的距离公式和直线与圆相切可得$\frac{{|{-3k+4}|}}{{\sqrt{{k^2}+1}}}=1$,
解得$k=\frac{{6±\sqrt{6}}}{4}$,∴${k_{max}}=\frac{{6+\sqrt{6}}}{4}$.
故答案为:$\frac{{6+\sqrt{6}}}{4}$
点评 本题考查三角函数的最值,转化为直线的斜率以及直线和圆相切是解决问题的关键,属基础题.

练习册系列答案
相关题目
12.正方体ABCD-A1B1C1D1中,E是棱BB1中点,G是DD1中点,F是BC上一点且FB=$\frac{1}{4}$BC,则GB与EF所成的角为( )
| A. | 30° | B. | 120° | C. | 60° | D. | 90° |
9.若函数f(x)=x2-x+1,x∈[-1,1],不等式f(x)>2x+m恒成立,则m的取值范围是( )
| A. | (-∞,-1) | B. | (-∞,3) | C. | (-1,3) | D. | (3,+∞) |
 在区间
在区间 上单调递增,则实数
上单调递增,则实数 的取值范围是__________.
的取值范围是__________.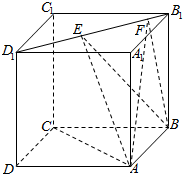 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的个数是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的个数是( )