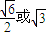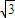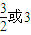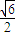题目内容
已知双曲线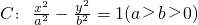 半焦距为c,过焦点且斜率为1的直线与双曲线C的左右两支各有一个交点,若抛物线y2=4cx的准线被双曲线C截得的弦长为
半焦距为c,过焦点且斜率为1的直线与双曲线C的左右两支各有一个交点,若抛物线y2=4cx的准线被双曲线C截得的弦长为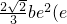 为双曲线C的离心率),则e的值为
为双曲线C的离心率),则e的值为
- A.
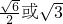
- B.

- C.
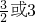
- D.

B
分析:抛物线y2=4cx的准线正好经过双曲线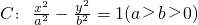 的左焦点,准线被双曲线C截得的弦长为
的左焦点,准线被双曲线C截得的弦长为 ,
,
由 =
= ,得出a和c的关系,从而求出离心率的值.
,得出a和c的关系,从而求出离心率的值.
解答:∵抛物线y2=4cx的准线:x=-c,
它正好经过双曲线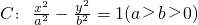 的左焦点,
的左焦点,
∴准线被双曲线C截得的弦长为:2 ,
,
∴2 =
= ,
,
即: c2=3ab,又
c2=3ab,又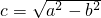
∴解得:e= 的值为:
的值为: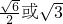 ,
,
又过焦点且斜率为1的直线与双曲线C的左右两支各有一个交点,
∴e= .
.
故选B.
点评:本题考查直线方程、椭圆的方程、直线和椭圆的位置关系.由圆锥曲线的方程求焦点、离心率、双曲线的三参数的关系:c2=a2+b2注意双曲线与椭圆的区别.
分析:抛物线y2=4cx的准线正好经过双曲线
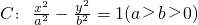 的左焦点,准线被双曲线C截得的弦长为
的左焦点,准线被双曲线C截得的弦长为 ,
,由
 =
= ,得出a和c的关系,从而求出离心率的值.
,得出a和c的关系,从而求出离心率的值.解答:∵抛物线y2=4cx的准线:x=-c,
它正好经过双曲线
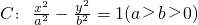 的左焦点,
的左焦点,∴准线被双曲线C截得的弦长为:2
 ,
,∴2
 =
= ,
,即:
 c2=3ab,又
c2=3ab,又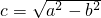
∴解得:e=
 的值为:
的值为: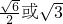 ,
,又过焦点且斜率为1的直线与双曲线C的左右两支各有一个交点,
∴e=
 .
.故选B.
点评:本题考查直线方程、椭圆的方程、直线和椭圆的位置关系.由圆锥曲线的方程求焦点、离心率、双曲线的三参数的关系:c2=a2+b2注意双曲线与椭圆的区别.

练习册系列答案
相关题目
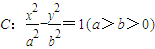 半焦距为c,过焦点且斜率为1的直线与双曲线C的左右两支各有一个交点,若抛物线y2=4cx的准线被双曲线C截得的弦长为
半焦距为c,过焦点且斜率为1的直线与双曲线C的左右两支各有一个交点,若抛物线y2=4cx的准线被双曲线C截得的弦长为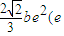 为双曲线C的离心率),则e的值为( )
为双曲线C的离心率),则e的值为( )