题目内容
 某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106),已知样本中产品净重小于100克的个数是24,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106),已知样本中产品净重小于100克的个数是24,则样本中净重大于或等于98克并且小于104克的产品的个数是( )| A、90 | B、75 | C、60 | D、45 |
考点:频率分布直方图
专题:概率与统计
分析:由频率分布直方图,求出样本容量,再求出净重大于或等于98克并且小于104克的产品的频率与频数.
解答:
解:根据频率分布直方图知,样本中产品净重小于100克的频率是
(0.050+0.100)×2=0.3,
∴样本容量是
=80;
∴样本中净重大于或等于98克并且小于104克的产品的频率是
(0.100+0.150+0.125)×2=0.75,
∴对应的频数为
80×0.75=60.
故选:C.
(0.050+0.100)×2=0.3,
∴样本容量是
| 24 |
| 0.3 |
∴样本中净重大于或等于98克并且小于104克的产品的频率是
(0.100+0.150+0.125)×2=0.75,
∴对应的频数为
80×0.75=60.
故选:C.
点评:本题考查了频率分布直方图的应用问题,根据频率分布直方图求出样本的容量,是解题的关键,属于基础题.

练习册系列答案
相关题目
数0与集合∅的关系是( )
| A、0∈∅ | B、0=∅ |
| C、0∉∅ | D、{0}=∅ |
设不等式|x-a|<b解集是{x|-1<x<2},则a与b的值是( )
| A、a=1,b=3 | ||||
| B、a=-1,b=3 | ||||
| C、a=-1,b=-3 | ||||
D、a=
|
函数f(x)=x2-2ax-3在区间(-8,2)上为减函数,则有( )
| A、a∈(-∞,1] |
| B、a∈[2,+∞) |
| C、a∈[1,2] |
| D、a∈(-∞,1]∪[2,+∞) |
(文科)已知F1、F2是椭圆
+
=1(a>b>0)的两个焦点,若椭圆上存在点P,满足∠F1PF2=120°,则
的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| b |
A、(
| ||
B、(
| ||
C、[
| ||
D、(1,
|
设x0是方程lnx+x=4的解,则x0在下列哪个区间内( )
| A、(3,4) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
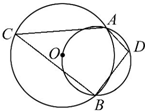 如图,两圆相交于A,B两点,小圆经过大圆的圆心O,点C,D分别在两圆上,若∠ADB=100°,则∠ACB的度数为( )
如图,两圆相交于A,B两点,小圆经过大圆的圆心O,点C,D分别在两圆上,若∠ADB=100°,则∠ACB的度数为( )| A、35° | B、40° |
| C、50° | D、80° |
在平面直角坐标系中,设M(-3,2)、N(2,-3),沿x轴把坐标平面折成90°的二面角后,则|
|的长为( )
| MN |
A、
| ||
B、
| ||
C、2
| ||
D、5
|
对于集合M,N,定义M-N={x|x∈M,且x∉N},设A={x|x≥-
},B={x|x<0},则B-A等于( )
| 9 |
| 4 |
A、(-∞,-
| ||
B、(-∞,-
| ||
| C、(0,+∞) | ||
| D、[0,+∞) |