题目内容
曲线y=x2和y2=x所围成的平面图形绕x轴旋转一周后,所形成的旋转体的体积为
- A.

- B.

- C.

- D.
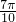
A
分析:欲求曲线y=x2和y2=x所围成的平面图形绕x轴旋转一周后所形成的旋转体的体积,可利用定积分计算,即求出被积函数y=π(x-x4)在0→1上的积分即可.
解答:设旋转体的体积为V,
则 01
01
= .
.
故旋转体的体积为: .
.
故选A.
点评:本小题主要考查定积分、定积分的应用等基础知识,考查数形结合思想.属于基础题.
分析:欲求曲线y=x2和y2=x所围成的平面图形绕x轴旋转一周后所形成的旋转体的体积,可利用定积分计算,即求出被积函数y=π(x-x4)在0→1上的积分即可.
解答:设旋转体的体积为V,
则
 01
01=
 .
.故旋转体的体积为:
 .
.故选A.
点评:本小题主要考查定积分、定积分的应用等基础知识,考查数形结合思想.属于基础题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
曲线y=x2和y2=x所围成的平面图形绕x轴旋转一周后,所形成的旋转体的体积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|