题目内容
设F是双曲线C:
-
=1(a>0,b>0)的右焦点,直线y=
x交双曲线左右两支于M,N,若|OM|=|OF|,则双曲线的离心率等于
+1
+1.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 3 |
| 3 |
分析:根据直线的斜率公式,得∠NOF=60°,所以△ONF是以c为边长的等边三角形,得点N(
c,
c),代入双曲线方程并化简整理,得关于离心率e的方程,解之可得该双曲线的离心率.
| 1 |
| 2 |
| ||
| 2 |
解答:解: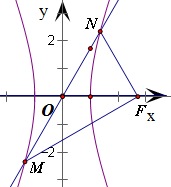 ∵直线y=
∵直线y=
x交双曲左右两支于M,N,且|OM|=|OF|,
∴由tan∠NOF=
,得∠NOF=60°,且|ON|=|OF|,
因此△ONF是以c为边长的等边三角形,
得N(
c,
c),代入双曲线方程得
-
=1
即:
-
=1,将e=
和b2=c2-a2代入化简整理,
得
e2-
•
=1,解之得e2=4±2
∴双曲线的离心率e=
+1(因为双曲线离心率e>1,舍去
-1)
故答案为:
+1
 ∵直线y=
∵直线y=| 3 |
∴由tan∠NOF=
| 3 |
因此△ONF是以c为边长的等边三角形,
得N(
| 1 |
| 2 |
| ||
| 2 |
(
| ||
| a2 |
(
| ||||
| b2 |
即:
| c2 |
| 4a2 |
| 3c2 |
| 4b2 |
| c |
| a |
得
| 1 |
| 4 |
| 3 |
| 4 |
| e2 |
| e2-1 |
| 3 |
∴双曲线的离心率e=
| 3 |
| 3 |
故答案为:
| 3 |
点评:本题给出直线y=
x交双曲线于M、N两点,且在|ON|=c的情况下求双曲线的离心率,着重考查了双曲线的简单性质和直线与双曲线位置关系等知识,属于基础题.
| 3 |

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
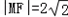 ,求点M的坐标;
,求点M的坐标; )的直线l交C于P、Q两点,若l与圆x2+y2=1相切,求证:OP⊥OQ。
)的直线l交C于P、Q两点,若l与圆x2+y2=1相切,求证:OP⊥OQ。 ,求直线l的方程.
,求直线l的方程.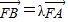 ,当λ∈[6,+∞)时,求直线l的斜率k的取值范围.
,当λ∈[6,+∞)时,求直线l的斜率k的取值范围.