题目内容
已知点F是双曲线C:x2-y2=2的左焦点,直线l与双曲线C交于A、B两点,
(1)若直线l过点P(1,2),且
+
=2
,求直线l的方程.
(2)若直线l过点F且与双曲线的左右两支分别交于A、B两点,设
=λ
,当λ∈[6,+∞)时,求直线l的斜率k的取值范围.
(1)若直线l过点P(1,2),且
| OA |
| OB |
| OP |
(2)若直线l过点F且与双曲线的左右两支分别交于A、B两点,设
| FB |
| FA |
分析:(1)由A、B两点在双曲线上,代入双曲线方程,利用点差法,结合
+
=2
,可求直线l的斜率,进而可求方程.
(2)根据
=λ
,可得坐标关系,将直线方程代入双曲线方程,从而可得关于λ的函数,从而可求直线l的斜率k的取值范围.
| OA |
| OB |
| OP |
(2)根据
| FB |
| FA |
解答:解:设A(x1,y2),B(x2,y2),
(1)由A、B两点在双曲线上,得
作差:(x1-x2)(x1+x2)=(y1-y2)(y1+y2)即
=
,
由
+
=2
,知
则直线l的斜率k=
,直线l的方程为y-2=
(x-1)即x-2y+3=0
易知直线l与双曲线有两个交点,方程x-2y+3=0即为所求,
(2)F(-2,0),由
=λ
,得
设直线l:y=k(x+2),由
,得(1-k2)y2-4ky+2k2=0.
∴△=16k2-8k2(1-k2)=8k2(1+k2)y1+y2=
,y1y2=
.
由y2=λy1,y1+y2=
,y1y2=
,消去y1,y2,
得
=
=λ+
+2.
∵λ≥6,函数g(λ)=λ+
+2在(1,+∞)上单调递增,
∴
≥6+
+2=
,∴k2≥
.
又直线l与双曲线的两支相交,即方程(1-k2)y2-4ky+2k2=0两根同号,
∴k2<1.
∴
≤k2<1,故k∈(-1,-
]∪[
,1).
(1)由A、B两点在双曲线上,得
|
作差:(x1-x2)(x1+x2)=(y1-y2)(y1+y2)即
| y1-y2 |
| x1-x2 |
| x1+x2 |
| y1+y2 |
由
| OA |
| OB |
| OP |
|
则直线l的斜率k=
| 1 |
| 2 |
| 1 |
| 2 |
易知直线l与双曲线有两个交点,方程x-2y+3=0即为所求,
(2)F(-2,0),由
| FB |
| FA |
|
设直线l:y=k(x+2),由
|
∴△=16k2-8k2(1-k2)=8k2(1+k2)y1+y2=
| 4k |
| 1-k2 |
| 2k2 |
| 1-k2 |
由y2=λy1,y1+y2=
| 4k |
| 1-k2 |
| 2k2 |
| 1-k2 |
得
| 8 |
| 1-k2 |
| (1+λ)2 |
| λ |
| 1 |
| λ |
∵λ≥6,函数g(λ)=λ+
| 1 |
| λ |
∴
| 8 |
| 1-k2 |
| 1 |
| 6 |
| 49 |
| 6 |
| 1 |
| 49 |
又直线l与双曲线的两支相交,即方程(1-k2)y2-4ky+2k2=0两根同号,
∴k2<1.
∴
| 1 |
| 49 |
| 1 |
| 7 |
| 1 |
| 7 |
点评:本题以双曲线为载体,考查直线与双曲线的位置关系,考查点差法,关键是设点代入作差.

练习册系列答案
相关题目
已知点F是双曲线
-
=1(a>0,b>0)的右焦点,点C是该双曲线的左顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABC是锐角三角形,则此双曲线离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、(1,2) | ||
| B、(1,+∞) | ||
C、(2,1+
| ||
D、(1,1+
|
 ,求直线l的方程.
,求直线l的方程.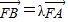 ,当λ∈[6,+∞)时,求直线l的斜率k的取值范围.
,当λ∈[6,+∞)时,求直线l的斜率k的取值范围.