题目内容
已知函数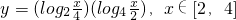
(1)求当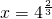 时对应的y值;
时对应的y值;
(2)求函数y的最大值和最小值,并求出此时x的值.
解:(1)y= (log2x-2)(log2x-1)
(log2x-2)(log2x-1)
当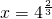 时,
时, (
( -2)(
-2)( -1)=
-1)= ×(-
×(- )=
)=
(2)令log2x=t,x∈[2,4]则t∈[1,2]
∴
= ①
①
 时
时 此时
此时
t=1或2时,ymax=0此时x=2或4.
分析:(1)先根据对数的运算性质进行化简,然后将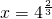 代入进行求解即可;
代入进行求解即可;
(2)令log2x=t,根据x的范围求出t的范围,转化成关于t的二次函数,然后进行配方得到对称轴,根据二次函数的性质可求出函数y的最值,然后求出相应的x即可.
点评:本题主要考查了对数的运算性质,同时考查了换元法的应用,转化与划归的数学思想,属于基础题.
 (log2x-2)(log2x-1)
(log2x-2)(log2x-1)当
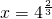 时,
时, (
( -2)(
-2)( -1)=
-1)= ×(-
×(- )=
)=
(2)令log2x=t,x∈[2,4]则t∈[1,2]
∴

=
 ①
① 时
时 此时
此时
t=1或2时,ymax=0此时x=2或4.
分析:(1)先根据对数的运算性质进行化简,然后将
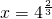 代入进行求解即可;
代入进行求解即可;(2)令log2x=t,根据x的范围求出t的范围,转化成关于t的二次函数,然后进行配方得到对称轴,根据二次函数的性质可求出函数y的最值,然后求出相应的x即可.
点评:本题主要考查了对数的运算性质,同时考查了换元法的应用,转化与划归的数学思想,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
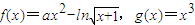
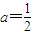 时,证明:对x∈(0,1)时,不等式2f(x)<g(x)成立;
时,证明:对x∈(0,1)时,不等式2f(x)<g(x)成立;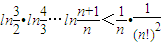 .
.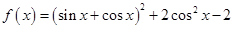 .
.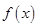 的最小正周期;
的最小正周期;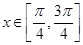 时,求函数
时,求函数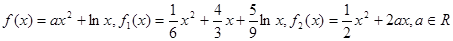 .
. 在点
在点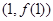 处的切线方程;
处的切线方程;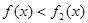 在区间
在区间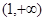 上恒成立,求
上恒成立,求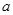 的取值范围;
的取值范围;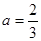 时,求证:在区间
时,求证:在区间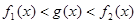 恒成立的函数
恒成立的函数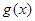 有无穷多个.
有无穷多个. .
. 的单调区间;
的单调区间; 上的最小值;
上的最小值; ,当
,当 时,对任意
时,对任意 ,都有
,都有 成立,求实数
成立,求实数 的取值范围。
的取值范围。