题目内容
已知函数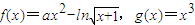
(1)求函数f(x)的单调区间;
(2)当
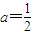 时,证明:对x∈(0,1)时,不等式2f(x)<g(x)成立;
时,证明:对x∈(0,1)时,不等式2f(x)<g(x)成立;(3)当n≥2,,n∈N*证明:
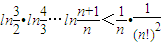 .
.
【答案】分析:(1)求出f(x)的导函数和f(x)的定义域,并求出导函数分子中多项式的根的判别式,分a小于等于0大于等于-1,a大于0和a小于-1三种情况讨论导函数的正负和根的判别式的正负即可得到函数的单调区间;
(2)设h(x)=2f(x)-g(x),把f(x)和g(x)的解析式代入h(x)中确定出h(x),求出h(x)的导函数,得到导函数小于0即h(x)为减函数,得到h(x)小于h(0),而h(0)=0,化简得证;
(3)由(2)中的h(x)小于0得到ln(x+1)小于x2-x3,令x= ,即可得到
,即可得到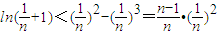 ,同理把n换成n-1,n-2,…,2,把所有的不等式相乘,约分化简后得证.
,同理把n换成n-1,n-2,…,2,把所有的不等式相乘,约分化简后得证.
解答:解(1) (x>-1),△=16a(a+1),
(x>-1),△=16a(a+1),
①-1≤a≤0时,△<0,f′(x)<0,单调减区间(-1,+∞);
②a>0时,△>0,单调减区间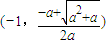 ;增区间
;增区间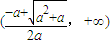 ;
;
③a<-1时,△>0,单调减区间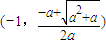 ∪
∪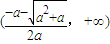 ;增区间
;增区间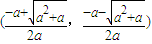 ;
;
(2)设h(x)=2f(x)-g(x)=x2-ln(x+1)-x3,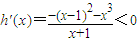 ,
,
所以h(x)<h(0)=0,即2f(x)<g(x),
(3)由(2)ln(x+1)<x2-x3,
令 ,则
,则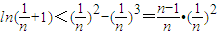 ,
,
同理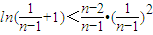 ,…,
,…,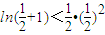 ,累乘即得证.
,累乘即得证.
点评:此题考查学生会利用导函数的正负得到函数的单调区间,掌握导数在最值问题中的应用,是一道综合题.
(2)设h(x)=2f(x)-g(x),把f(x)和g(x)的解析式代入h(x)中确定出h(x),求出h(x)的导函数,得到导函数小于0即h(x)为减函数,得到h(x)小于h(0),而h(0)=0,化简得证;
(3)由(2)中的h(x)小于0得到ln(x+1)小于x2-x3,令x=
 ,即可得到
,即可得到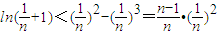 ,同理把n换成n-1,n-2,…,2,把所有的不等式相乘,约分化简后得证.
,同理把n换成n-1,n-2,…,2,把所有的不等式相乘,约分化简后得证.解答:解(1)
 (x>-1),△=16a(a+1),
(x>-1),△=16a(a+1),①-1≤a≤0时,△<0,f′(x)<0,单调减区间(-1,+∞);
②a>0时,△>0,单调减区间
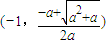 ;增区间
;增区间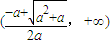 ;
;③a<-1时,△>0,单调减区间
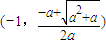 ∪
∪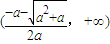 ;增区间
;增区间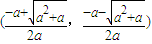 ;
;(2)设h(x)=2f(x)-g(x)=x2-ln(x+1)-x3,
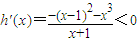 ,
,所以h(x)<h(0)=0,即2f(x)<g(x),
(3)由(2)ln(x+1)<x2-x3,
令
 ,则
,则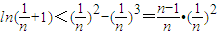 ,
,同理
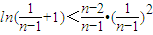 ,…,
,…,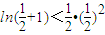 ,累乘即得证.
,累乘即得证.点评:此题考查学生会利用导函数的正负得到函数的单调区间,掌握导数在最值问题中的应用,是一道综合题.

练习册系列答案
相关题目



 的极值点;
的极值点; 过点(0,—1),并且与曲线
过点(0,—1),并且与曲线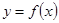 相切,求直线
相切,求直线 ,其中
,其中 ,求函数
,求函数 在
在 上的最小值.(其中e为自然对数的底数)
上的最小值.(其中e为自然对数的底数)