题目内容
(本题满分16分)
已知函数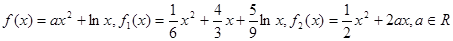 .
.
(1)求函数 在点
在点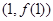 处的切线方程;
处的切线方程;
(2)若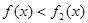 在区间
在区间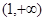 上恒成立,求
上恒成立,求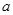 的取值范围;
的取值范围;
(3)当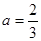 时,求证:在区间
时,求证:在区间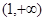 上,满足
上,满足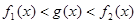 恒成立的函数
恒成立的函数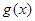 有无穷多个.
有无穷多个.
【答案】
(1)因为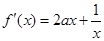 ,
,
所以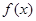 在点
在点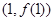 处的切线的斜率为
处的切线的斜率为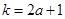 ,……2分
,……2分
所以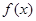 在点
在点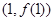 处的切线方程为
处的切线方程为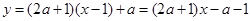 , 4分
, 4分
(2) 令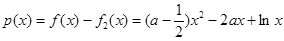 <0,对
<0,对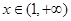 恒成立,
恒成立,
因为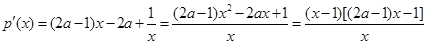 (*)
(*)
………………………………………………………………6分
①当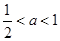 时,有
时,有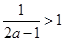 ,即
,即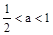 时,在(
时,在(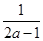 ,+∞)上有
,+∞)上有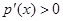 ,
,
此时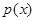 在区间(
在区间(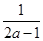 ,+∞)上是增函数,
,+∞)上是增函数,
并且在该区间上有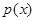 ∈
∈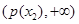 ,不合题意;
,不合题意;
②当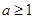 时,有
时,有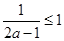 ,同理可知,
,同理可知,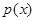 在区间
在区间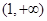 上,有
上,有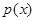 ∈
∈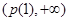 ,
,
也不合题意; …………………………………………… 8分
③当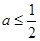 时,有
时,有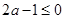 ,此时在区间
,此时在区间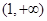 上恒有
上恒有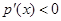 ,
,
从而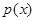 在区间
在区间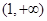 上是减函数;
上是减函数;
要使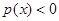 在此区间上恒成立,只须满足
在此区间上恒成立,只须满足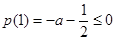
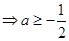 ,
,
所以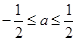 .
………………………………………11分
.
………………………………………11分
综上可知 的范围是
的范围是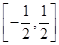 . ………………………………………12分
. ………………………………………12分
(3)当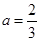 时,
时,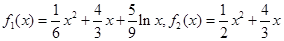
记 .
.
因为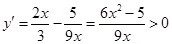 ,所以
,所以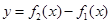 在
在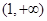 上为增函数,
上为增函数,
所以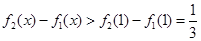 ,
………………………………14分
,
………………………………14分
设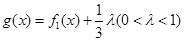 ,
则
,
则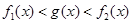 , 所以在区间
, 所以在区间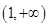 上,
上,
满足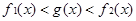 恒成立的函数
恒成立的函数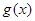 有无穷多个. …………………16分
有无穷多个. …………………16分
【解析】略

练习册系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在