题目内容
已知经过A（-2，0）和点B（1，3a）的直线l1与经过点P（0，-1）和点Q（a，-2a）的直线l2互相垂直，求实数a的值．
考点：直线的一般式方程与直线的垂直关系
专题：直线与圆
分析：对a分类讨论．利用两条直线相互垂直与斜率的关系即可得出．
解答：
解：当a=0时，直线l1的斜率为0，直线l2的斜率不存在，此时两条直线相互垂直，满足题意，因此a=0．
当a≠0时，直线l1的斜率=
=a，直线l2的斜率=
=
，由于两条直线相互垂直，∴a×
=-1，解得a=1．
综上可得：实数a=1或1．
当a≠0时，直线l1的斜率=
| 3a |
| 3 |
| -1+2a |
| -a |
| 1-2a |
| a |
| 1-2a |
| a |
综上可得：实数a=1或1．
点评：本题考查了直线相互垂直与斜率的关系、分类讨论思想方法，考查了计算能力，属于基础题．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
已知a，b，c分别为△ABC的三个内角A，B，C的对边，若a=2
，b=2
，A=60°，则角B等于（ ）
| 3 |
| 2 |
| A、45°或135° | B、135° |
| C、60° | D、45° |
“m=4”是“直线mx+（1-m）y+1=0和直线3x+my-1=0垂直”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在平面直角坐标系中，A（0，0），B（1，2）两点绕定点P顺时针旋转θ角分别到A′（4，4），B′（5，2）两点，则cosθ的值为（ ）
| A、0 | ||
B、-
| ||
C、-
| ||
D、-
|
“cos2α=-
”是“α=kπ+
，k∈Z”的（ ）
| ||
| 2 |
| 5π |
| 12 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若i为虚数单位，则i+i2+i3+i4的值为（ ）
| A、-1 | B、i | C、0 | D、1 |
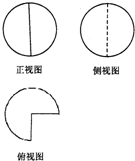一个半径为1的球体经过切割后，剩余部分几何体的三视图如图所示，则该几何体的表面积为（ ）| A、16π | ||
| B、14π | ||
| C、4π | ||
D、
|