题目内容
已知z1=(1-sinθ)+i,其中i为虚数单位,θ∈R.(1)求|z1|的取值范围;
(2)如果z1和z2=
| 1 |
| 4(1+sinθ) |
| 1 |
| 2cosθ |
分析:(1)由复数模的计算公式,结合z1=(1-sinθ)+i,我们易写出|z1|的表达式,进而将问题转化为一个求函数值域的问题,结合三角函数的性质,我们易得|z1|的取值范围;
(2)根据互为共轭复数的两个复数实部相等,虚部相反,我们可以构造一个三角方程,解方程即可求出满足条件的cosθ的值.
(2)根据互为共轭复数的两个复数实部相等,虚部相反,我们可以构造一个三角方程,解方程即可求出满足条件的cosθ的值.
解答:解:(1)∵z1=(1-sinθ)+i,
∴|z1|=
,
∴当sinθ=1时,|z1|取最小值1,
当sinθ=-1时,|z1|取最大值
,
所以|z1|取值范围为[1,
].
(2)由条件得
,
∴cosθ=
.
∴|z1|=
| (1-sinθ)2+1 |
∴当sinθ=1时,|z1|取最小值1,
当sinθ=-1时,|z1|取最大值
| 5 |
所以|z1|取值范围为[1,
| 5 |
(2)由条件得
|
∴cosθ=
| 1 |
| 2 |
点评:本题考查的知识点是复数求模,及复数的基本概率中共轭复数的定义.
(1)中重要的熟练掌握三角函数的性质;
(2)中根据共轭复数的两个复数实部相等,虚部相反,构造方程是解答本题的关键.
(1)中重要的熟练掌握三角函数的性质;
(2)中根据共轭复数的两个复数实部相等,虚部相反,构造方程是解答本题的关键.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
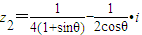 互为共轭复数,求cosθ的值.
互为共轭复数,求cosθ的值.