题目内容
14.一个正四棱锥的内切球半径为1,则此正四棱锥体积的最小值为$\frac{32}{3}$.分析 先求出正四棱锥体积,再利用导数知识求解即可.
解答 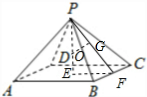 解:设正四棱锥的高为h,底边长为2a,则斜高为$\sqrt{{a}^{2}+{h}^{2}}$,
解:设正四棱锥的高为h,底边长为2a,则斜高为$\sqrt{{a}^{2}+{h}^{2}}$,
∵正四棱锥的内切球半径为1,
∴由△POG∽△PFE可得$\frac{1}{h-1}=\frac{a}{\sqrt{{a}^{2}+{h}^{2}}}$,
∴a2=$\frac{{h}^{2}}{{h}^{2}-2h}$
∴正四棱锥体积V=$\frac{1}{3}×4{a}^{2}h$=$\frac{4}{3}$×$\frac{{h}^{3}}{{h}^{2}-2h}$,
V′=$\frac{{h}^{3}(h-4)}{({h}^{2}-2h)^{2}}$,
∴0<h<4时,V′<0;h>4时,V′>0,
∴h=4时,正四棱锥体积取得最小值,最小值为$\frac{32}{3}$.
故答案为:$\frac{32}{3}$.
点评 本题主要考查球与正四棱锥的关系,考查导数知识的运用,正确求出正四棱锥体积是关键.

练习册系列答案
相关题目
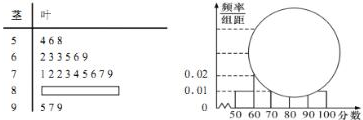 某校高一某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题;
某校高一某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题;
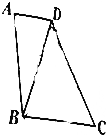 在直角梯形ABCD中,AD∥BC,∠A=90°,AB=2AD,若将△ABD沿直线BD折成△A′BD,使得A′D⊥BC,则直线A′B与平面BCD所成角的正弦值是$\frac{\sqrt{3}}{4}$.
在直角梯形ABCD中,AD∥BC,∠A=90°,AB=2AD,若将△ABD沿直线BD折成△A′BD,使得A′D⊥BC,则直线A′B与平面BCD所成角的正弦值是$\frac{\sqrt{3}}{4}$.