题目内容
7.某中学高二年级共有6个班,现从外地转入4名学生,要安排到该年级的两个班级,且每班安排两名,则不同的安排方案种数为( )| A. | A${\;}_{4}^{2}$•C${\;}_{4}^{2}$ | B. | $\frac{1}{2}$A${\;}_{6}^{2}$•C${\;}_{4}^{2}$ | C. | A${\;}_{6}^{2}$•C${\;}_{4}^{2}$ | D. | 2A${\;}_{6}^{2}$ |
分析 首先将4名学生均分成两组,选择完成以后要除以2,再从6个班级中选出2个班进行排列,最后根据分步计数原理得到合要求的安排方法数.
解答 解:由题意知本题是一个排列组合及简单计数问题
首先将4名学生均分成两组方法数为$\frac{1}{2}$C42,
再分配给6个班级中的2个分配方法数为A62,
∴根据分步计数原理合要求的安排方法数为$\frac{1}{2}$A62C42,
故选:B.
点评 本题考查的是平均分组问题,解题的关键是在平均分组时,选择完成以后要除以2,即去掉重复的部分,本题是一个基础题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
17.函数f(x)=∫${\;}_{0}^{x}$t(t-4)dt在[-1,5]上( )
| A. | 有最大值,无最小值 | B. | 有最大值和最小值 | ||
| C. | 有最小值,无最大值 | D. | 无最值 |
18.命题“|x|≥0(x∈R)”的否定是( )
| A. | “?x∈R,使|x|<0” | B. | “?x∈R,使|x|<0” | C. | “?x∉R,使|x|<0” | D. | “?x∈R,使|x|≤0” |
15.从甲、乙、丙、丁、戊五人中任选三人作代表,这五人入选的机会均等,则甲或乙被选中的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{10}$ |
16.曲线y=$\frac{1}{x}$及直线y=x,y=2所围成的图形面积为( )
| A. | 3+ln2 | B. | 3-ln2 | C. | $\frac{3}{2}$+ln2 | D. | $\frac{3}{2}$-ln2 |
17.独立性检验中,假设命题H0:变量X与变量Y没有关系.则在H0成立的情况下,则 k2≥5.024表示的意义是( )
| A. | 变量X与变量Y有关系的概率为2.5% | |
| B. | 变量X与变量Y没有关系的概率为97.5% | |
| C. | 变量X与变量Y有关系的概率为97.5% | |
| D. | 变量X与变量Y没有关系的概率为99% |
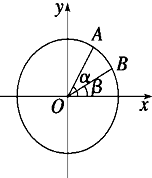 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A、B两点.已知A、B的横坐标分别为x1,x2.
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A、B两点.已知A、B的横坐标分别为x1,x2.