题目内容
2.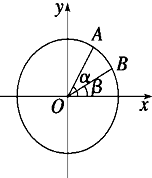 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A、B两点.已知A、B的横坐标分别为x1,x2.
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A、B两点.已知A、B的横坐标分别为x1,x2.(Ⅰ)若x1=$\frac{{3\sqrt{10}}}{10}$,x2=$\frac{{7\sqrt{2}}}{10}$,求2α+β的值;
(Ⅱ)若x1=$\frac{3}{5}$,若角-β终边与单位圆交于C点,且$\overrightarrow{OA}•\overrightarrow{OC}$=0,求sin(α+β).
分析 (Ⅰ)由条件利用任意角的三角函数的定义,求得cosα、cosβ 的值,再利用同角三角函数的基本关系、二倍角公式求得cos2α、sin2α、sinβ 的值,从而求得 cos(2α+β)的值,进而求得2α+β的值.
(Ⅱ)由条件求得$\overrightarrow{OA}$的坐标,结合$\overrightarrow{OA}•\overrightarrow{OC}$=0求得$\overrightarrow{OC}$ 的坐标,可得α、β的正弦值和余弦值,再根据sin(α+β)的值求得α+β的值.
解答 解:(Ⅰ)若x1=$\frac{{3\sqrt{10}}}{10}$,x2=$\frac{{7\sqrt{2}}}{10}$,则cosα=x1=$\frac{{3\sqrt{10}}}{10}$,cosβ=x2=$\frac{{7\sqrt{2}}}{10}$,
∴cos2α=2cos2α-1=$\frac{4}{5}$,sin2α=2sinαcosα=2$\sqrt{{1-cos}^{2}α}$cosα=$\frac{3}{5}$,sinβ=$\sqrt{{1-cos}^{2}β}$=$\frac{\sqrt{2}}{10}$,
∴cos(2α+β)=cos2αcosβ-sin2αsinβ=$\frac{4}{5}$×$\frac{7\sqrt{2}}{10}$-$\frac{3}{5}$×$\frac{\sqrt{2}}{10}$=$\frac{\sqrt{2}}{2}$,
∴2α+β=$\frac{π}{4}$.
(Ⅱ)若x1=$\frac{3}{5}$,则cosα=x1=$\frac{3}{5}$,sinα=$\sqrt{{1-cos}^{2}α}$=$\frac{4}{5}$,即$\overrightarrow{OA}$=($\frac{3}{5}$,$\frac{4}{5}$).
若角-β终边与单位圆交于C点,且$\overrightarrow{OA}•\overrightarrow{OC}$=0,则$\overrightarrow{OC}$=($\frac{4}{5}$,-$\frac{3}{5}$),即cos(-β)=cosβ=$\frac{4}{5}$,
sin(-β)=-sinβ=-$\frac{3}{5}$,即sinβ=$\frac{3}{5}$,
∴sin(α+β)=sinαcosβ+cosαsinβ=$\frac{4}{5}$×$\frac{4}{5}$+$\frac{3}{5}$×$\frac{3}{5}$=1.
点评 本题主要考查任意角的三角函数的定义,同角三角函数的基本关系,两角差的正弦公式的应用,属于中档题.

| A. | -2009 | B. | -3010 | C. | -3014 | D. | 3028 |
| A. | A${\;}_{4}^{2}$•C${\;}_{4}^{2}$ | B. | $\frac{1}{2}$A${\;}_{6}^{2}$•C${\;}_{4}^{2}$ | C. | A${\;}_{6}^{2}$•C${\;}_{4}^{2}$ | D. | 2A${\;}_{6}^{2}$ |
| A. | $\frac{3\sqrt{17}}{2}$ | B. | 2$\sqrt{10}$ | C. | $\frac{13}{2}$ | D. | 3$\sqrt{10}$ |