题目内容
6．已知{an}是等差数列，Sn是其前n项和，若2a7-a5-3=0，则S17的值是51．分析 设等差数列{an}的公差为d，由2a7-a5-3=0，可得2（a1+6d）-（a1+4d）-3=0，化为：a9=3．利用S17=$\frac{17（{a}_{1}+{a}_{17}）}{2}$=17a9，即可得出．
解答 解：设等差数列{an}的公差为d，∵2a7-a5-3=0，∴2（a1+6d）-（a1+4d）-3=0，
化为：a1+8d=3，即a9=3．
则S17=$\frac{17（{a}_{1}+{a}_{17}）}{2}$=17a9=17×3=51．
故答案为：51．
点评 本题考查了等差数列通项公式与求和公式、方程的解法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
17．已知函数f（x）=cos2x的图象向左平移$φ（{0＜φ＜\frac{π}{2}}）$个单位后得到函数g（x）的图象，若使|f（x1）-g（x2）|=2成立x1，x2的满足${|{{x_1}-{x_2}}|_{min}}=\frac{π}{6}$，则φ的值为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{5π}{12}$ |
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象如图所示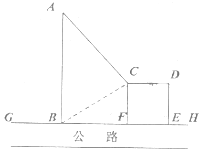
如图，GH是东西方向的公路北侧的边缘线，某公司准备在GH上的一点B的正北方向的A处建设一仓库，设AB=ykm，并在公路北侧建造边长为xkm的正方形无顶中转站CDEF（其中EF在GH上），现从仓库A向GH和中转站分别修两条道路AB，AC，已知AB=AC+1，且∠ABC=60°．．
18．已知等差数列{an}的前n项和为Sn，且S2=4，S4=16，数列{bn}满足bn=an+an+1，则数列{bn}的前9和T9为（ ）
| A． | 20 | B． | 80 | C． | 166 | D． | 180 |