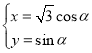题目内容
【题目】已知椭圆
的长轴长为
，焦距为2，抛物线
的准线经过C的左焦点F.
（1）求C与M的方程；
（2）直线l经过C的上顶点且l与M交于P，Q两点，直线FP，FQ与M分别交于点D（异于点P），E（异于点Q），证明:直线DE的斜率为定值.
【答案】（1）C：
，M：
（2）证明见解析
【解析】
（1）由题意可得
，
的值，运用
，求得
，可得椭圆
的方程，由
的准线经过点
，求得
，即可得解的方程；
（2）设直线
的方程为
，联立直线与抛物线的方程，设
，
，运用韦达定理得
之间的关系，再联立直线
与抛物线的方程解得
的坐标，同理可得出
的坐标，代入两点间斜率计算公式即可得结果.
（1）由题意，得
，
，所以
，
，
所以
，所以C的方程为，
所以
，由于M的准线经过点F，
所以
，所以
，故M的方程为.
（2）证明:由题意知，l的斜率存在，故设直线l的方程为，
由
，得
.
设，，
则
，即
且
，
，
.
又直线FP的方程为
，
由
，得
，
所以
，所以
，从而D的坐标为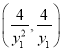
.
同理可得E的坐标为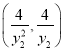
，
所以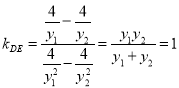
为定值.
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
【题目】某学校共有教职工120人，对他们进行年龄结构和受教育程度的调查，其结果如下表：
本科 | 研究生 | 合计 | |
35岁以下 | 40 | 30 | 70 |
35-50岁 | 27 | 13 | 40 |
50岁以上 | 8 | 2 | 10 |
现从该校教职工中任取1人，则下列结论正确的是（ ）
A.该教职工具有本科学历的概率低于60％
B.该教职工具有研究生学历的概率超过50％
C.该教职工的年龄在50岁以上的概率超过10％
D.该教职工的年龄在35岁及以上且具有研究生学历的概率超过10％
