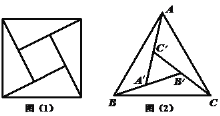题目内容
【题目】正方体ABCD﹣A1B1C1D1中，E是棱DD1的中点，F是侧面CDD1C1上的动点，且B1F∥平面A1BE，记B1与F的轨迹构成的平面为α.
①F，使得B1F⊥CD1
②直线B1F与直线BC所成角的正切值的取值范围是[
，
]
③α与平面CDD1C1所成锐二面角的正切值为2
④正方体ABCD﹣A1B1C1D1的各个侧面中，与α所成的锐二面角相等的侧面共四个.
其中正确命题的序号是_____.（写出所有正确的命题序号）
【答案】①②③④
【解析】
分别取CC1和C1D1的中点为M，N，连接MN、MB1、NB1，然后利用面面平行的判定定理证明平面MNB1∥平面A1BE，从而确定平面MNB1就是平面α.
当F为线段MN的中点时，可证明①；
②利用平移的思想，将直线B1F与直线BC所成角转化为B1F与B1C1所成的角，由于B1C1⊥平面MNC1，所以tan∠FB1C1即为所求，进而求解即可；
③平面MNB1与平面CDD1C1所成的锐二面角即为所求，也就是求出tan∠B1QC1即可；
④由正方体的对称性和二面角的含义即可判断.
解：如图所示，
设正方体的棱长为2，分别取CC1和C1D1的中点为M，N，连接MN、MB1、NB1，则MN∥A1B，MB1∥EA1，
∵MN、MB1平面MNB1，A1B、EA1平面A1BE，且MN∩MB1＝M，A1B∩EA1＝A1，
∴平面MNB1∥平面A1BE，
∴当F在MN上运动时，始终有B1F∥平面A1BE，即平面MNB1就是平面α.
对于①，当F为线段MN的中点时，∵MB1＝NB1，∴B1F⊥MN，∵MN∥CD1，∴B1F⊥CD1，即①正确；
对于②，∵BC∥B1C1，∴直线B1F与直线B1C1所成的角即为所求，
∵B1C1⊥平面MNC1，C1F平面MNC1，∴B1C1⊥C1F，
∴直线B1F与直线B1C1所成的角为∠FB1C1，且tan∠FB1C1
，
而FC1的取值范围为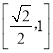
，B1C1＝2，所以tan∠FB1C1∈[
，
]，即②正确；
对于③，平面MNB1与平面CDD1C1所成的锐二面角即为所求，
取MN的中点Q，因为B1C1⊥平面MNC1，所以∠B1QC1就是所求角，
而tan∠B1QC1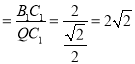
，即③正确；
对于④，由对称性可知，与α所成的锐二面角相等的面有平面BCC1B1，平面ADD1A1，平面A1B1C1D1，平面ABCD，即④正确.
故答案为：①②③④.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
