题目内容
已知正数数列 中,
中, ,前
,前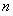 项和为
项和为 ,对任意
,对任意 ,
, 、
、 、
、 成等差数列.
成等差数列.
(1)求 和
和 ;
;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,当
,当 时,证明:
时,证明: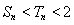 .
.
【答案】
(1)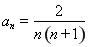 ,
,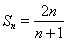 ;(2)证明过程详见试题解析.
;(2)证明过程详见试题解析.
【解析】
试题分析:(1)因为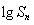 、
、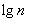 、
、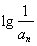 成等差数列,所以
成等差数列,所以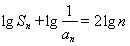 ,即
,即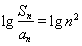 ,所以
,所以 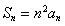 ,当
,当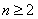 时,
时,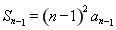 ,那么
,那么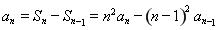 ,即
,即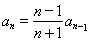 ,∴
,∴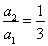 ,
,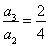 ,
,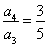 ,
,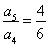 …
…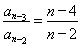 ,
,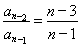 ,
,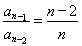 ,
,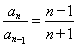 .
.
把以上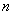 个式子相乘得:
个式子相乘得: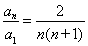 ,所以
,所以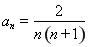 ,那么
,那么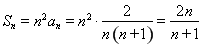 .(2)因为
.(2)因为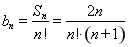 ,变形得
,变形得 ,那么可根据数列求和的列项相消法先求出
,那么可根据数列求和的列项相消法先求出 ,显然
,显然 ,又再根据
,又再根据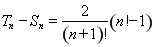 ,可知
,可知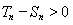 ,所以
,所以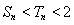 .
.
试题解析:(1)依题意: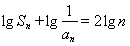 , 即
, 即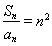 ,
,
∴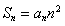 . ∴
. ∴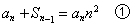 .
.
当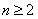 时,
时,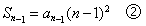
②代入①并整理得: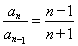
∴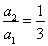 ,
,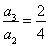 ,
,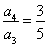 ,
,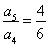 …
…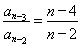 ,
,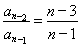 ,
,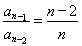
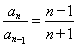
把以上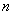 个式子相乘得:
个式子相乘得: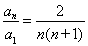 , 又∵
, 又∵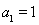
∴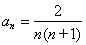
∵当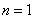 时,
时,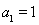 也满足上式,所以
也满足上式,所以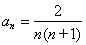
∵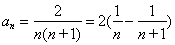
∴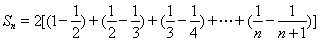
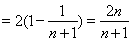
(2)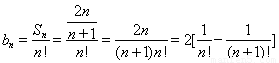
∴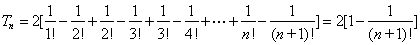
∵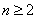 , ∴
, ∴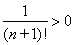 ,∴
,∴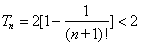
又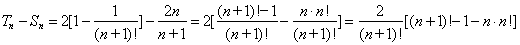
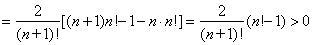
∴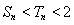 .
.
考点:数列的通项公式;数列的前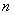 项和;证明数列不等式.
项和;证明数列不等式.

练习册系列答案
相关题目
 ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;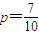 时,数列{bn}中是否存在最小项?若存在说明是第几项,如果不存在,说明理由.
时,数列{bn}中是否存在最小项?若存在说明是第几项,如果不存在,说明理由.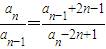 ,求
,求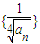 的前n项和为An,证明
的前n项和为An,证明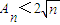 ;
;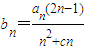 (c为非零常数),若数列{bn}是等差数列,其前n项和为Sn,求数列{(-1)nSn}的前m项和Tm.
(c为非零常数),若数列{bn}是等差数列,其前n项和为Sn,求数列{(-1)nSn}的前m项和Tm.