Question

已知正数数列{a_n}中，a₁=1，当n∈N^*，n≥2时满足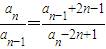，求
（1）求{a_n}的通项公式；
（2）记数列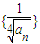的前n项和为A_n，证明；
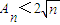（3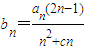）（c为非零常数），若数列{b_n}是等差数列，其前n项和为S_n，求数列{（-1）ⁿS_n}的前m项和T_m．

Answer 1

【答案】分析：对递推式进行变形得到：a_n-a_n-1=2n-1，再利用累加法求通项公式，本题（2）中的数列求和需要利用放缩法，放缩要恰到好处，这是难点之一．求数列{（-1）ⁿS_n}的前m项和T_m时，要先求出S_n再对n进行奇偶讨论．
解答：解：（1）交叉相乘⇒a_n=n²
（2）
∴
（3）⇒b_n=2n⇒S_n=n²+n
当m=2kT_m=-2（1-3）-4（3-5）-2k[（2k-1）-（2k+1）]=
当m=2k-1T_m=T_m+1-（-1）^m+1S_m+1=
∴
点评：本题（1）属于基础题目，另外2问较难一点，特别是放缩法的应用，得出t_m的值要进行讨论，并分段表示也是一个难点．