Question

已知正数数列{a_n}的前n 项和为S_n，且（p-1）S_n=p²-a_n，（n∈N^*，p＞0，p≠1），
（1）求数列{a_n}的通项公式；
（2）若，求数列{b_n}的前n项和T_n；
（3）当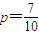时，数列{b_n}中是否存在最小项？若存在说明是第几项，如果不存在，说明理由．

Answer 1

【答案】分析：（1）由于正数数列{a_n}的前n 项和为S_n，且（p-1）S_n=p²-a_n，（n∈N^*，p＞0，p≠1），利用已知数列的前n项和求其通项的公式及等比数列的定义即可求得；
（2）有（1）再有若，利用错位相减法求得其前n项的和；
（3））当时，由于要求数列{b_n}中是否存在最小项，假设存在并设为第n项，利用解出该不等式组即可．
解答：解：（1）当n=1时，（P-1）a₁=P²-a₁，∴a₁=P
当n≥2时，（P-1）S_n=P²-a_n①
            （P-1）S_n-1=P²-a_n-1②

，
所以数列的等比数列．
∴等比数列a_n=P^2-n
（2），

∴∴．
（3）

即数列{b_n}中的最小项为第3项．
点评：此题考查了等比数列的定义，已知数列的前n项和求数列的通项，错位相减法求数列的前n项和，不等式的求解．