Question

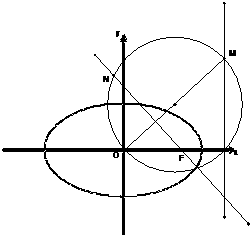（2011•石景山区一模）已知椭圆

x2

a2

+

y2

b2

=1经过点P（

6

2

，

1

2

），离心率是

2

2

，动点M（2，t）（t＞0）
（1）求椭圆的标准方程；
（2）求以OM为直径且别直线3x-4y-5=0截得的弦长为2的圆的方程；
（3）设F是椭圆的右焦点，过点F做OM的垂线与以OM为直径的圆交于点N，证明线段ON长是定值，并求出定值．

Answer 1

分析：（1）由椭圆

x2

a2

+

y2

b2

=1离心率是

2

2

，设椭圆方程设为

x2

4k2

+

y2

2k2

=1，把点P（

6

2

，

1

2

）代入，得

6 4

4k2

+

1 4

2k2

=1，由此能求出椭圆的标准方程．
（2）以OM为直径的圆的圆心是（1，

t

2

），半径r=

t2 4 +1

，方程为(x-1)2+(y-

t

2

)2=

t2

4

+1，由以OM为直径圆直线3x-4y-5=0截得的弦长为2，知

|3-2t-5|

5

=

t

2

，由此能求出所求圆的方程．
（3）设N（x₀，y₀），点N在以OM为直径的圆上，所以x₀²+y₀²=2x₀+ty₀，又N在过F垂直于OM的直线上，所以2x₀+ty₀=2，由此能求出ON．

解答：解：（1）∵椭圆

x2

a2

+

y2

b2

=1经过点P（

6

2

，

1

2

），
离心率是

2

2

，
∴椭圆方程设为

x2

4k2

+

y2

2k2

=1，
把点P（

6

2

，

1

2

）代入，
得

6 4

4k2

+

1 4

2k2

=1，
解得4k²=2，
∴椭圆的标准方程是

x2

2

+y2=1．
（2）以OM为直径的圆的圆心是（1，

t

2

），
半径r=

t2 4 +1

，
方程为(x-1)2+(y-

t

2

)2=

t2

4

+1，
∵以OM为直径圆直线3x-4y-5=0截得的弦长为2，
∴圆心（1，

t

2

）到直线3x-4y-5=0的距离d=

r2-1

=

t

2

，
∴

|3-2t-5|

5

=

t

2

，
解得t=4，
∴所求圆的方程是（x-1）²+（y-2）²=5．
（3）设N（x₀，y₀），
点N在以OM为直径的圆上，
所以x₀（x₀-2）+y₀（y₀-t）=0，
即：x₀²+y₀²=2x₀+ty₀，
又N在过F垂直于OM的直线上，
所以y0=-

2

t

(x0-1)，
即2x₀+ty₀=2，
所以ON=

2

．

点评：本题主要考查椭圆标准方程，简单几何性质，直线与椭圆的位置关系，圆的简单性质等基础知识．考查运算求解能力，推理论证能力；考查函数与方程思想，化归与转化思想．综合性强，难度大，易出错．解题时要认真审题，仔细解答．