Question

7．已知△ABC中，∠C为直角，D为边AC上一点，K为BD上一点，且∠ABC=∠KAD=∠AKD．证明：BK=2DC．

Answer 1

分析 设∠ABC=∠KAD=∠AKD=α，则tanα=$\frac{AC}{BC}$，tan2α=$\frac{BC}{CD}$=$\frac{2tanα}{1-{tan}^{2}α}$，进而可得CD=$\frac{{BC}^{2}-{AC}^{2}}{2AC}$，BK=$\frac{{BC}^{2}-{AC}^{2}}{AC}$，进而得到答案．

解答 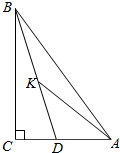证明：设∠ABC=∠KAD=∠AKD=α，
则tanα=$\frac{AC}{BC}$，tan2α=$\frac{BC}{CD}$=$\frac{2tanα}{1-{tan}^{2}α}$，
∴CD=$\frac{BC•（1-{tan}^{2}α）}{2tanα}$=$\frac{BC•[1-{（\frac{AC}{BC}）}^{2}]}{2•\frac{AC}{BC}}$=$\frac{{BC}^{2}-{AC}^{2}}{2AC}$，
则DK=AD=AC-CD=AC-$\frac{{BC}^{2}-{AC}^{2}}{2AC}$=$\frac{{3A{C}^{2}-BC}^{2}}{2AC}$，
∴BK=BD-DK=$\sqrt{{BC}^{2}+{CD}^{2}}$-DK=$\sqrt{{BC}^{2}+{（\frac{{BC}^{2}-{AC}^{2}}{2AC}）}^{2}}$-$\frac{{3A{C}^{2}-BC}^{2}}{2AC}$=$\frac{{BC}^{2}+{AC}^{2}}{2AC}$-$\frac{{3A{C}^{2}-BC}^{2}}{2AC}$=$\frac{{2BC}^{2}-2{AC}^{2}}{2AC}$=$\frac{{BC}^{2}-{AC}^{2}}{AC}$，
∴BK=2DC

点评 本题考查的知识点是二倍角的正切公式，三角函数的定义，勾股定理，难度中档．