题目内容
已知a≤
+lnx,对任意x∈[
,2]恒成立,则a的最大值 .
| 1-x |
| x |
| 1 |
| 2 |
考点:函数恒成立问题
专题:函数的性质及应用,不等式的解法及应用
分析:设f(x)=
+lnx,依题意,a≤f(x)min,利用导数法可求得f(x)=
+lnx的极小值,也是最小值,从而可得a的最大值.
| 1-x |
| x |
| 1-x |
| x |
解答:
解:设f(x)=
+lnx,
f′(x)=-
+
=
,
∵a≤
+lnx,对任意x∈[
,2]恒成立,
∴a≤f(x)min,
令f′(x)=0,得:x=1;
当
≤x<1时,f′(x)<0,f(x)=
+lnx单调递减;
当1<x≤2时,f′(x)>0,f(x)=
+lnx单调递增;
∴f(x)min=f(1)=0,
∴a≤0,
∴a的最大值为:0.
故答案为:0.
| 1-x |
| x |
f′(x)=-
| 1 |
| x2 |
| 1 |
| x |
| x-1 |
| x2 |
∵a≤
| 1-x |
| x |
| 1 |
| 2 |
∴a≤f(x)min,
令f′(x)=0,得:x=1;
当
| 1 |
| 2 |
| 1-x |
| x |
当1<x≤2时,f′(x)>0,f(x)=
| 1-x |
| x |
∴f(x)min=f(1)=0,
∴a≤0,
∴a的最大值为:0.
故答案为:0.
点评:本题考查函数恒成立问题,着重考查构造函数思想、等价转化思想与导数法求极值的综合应用,求得f(x)=
+lnx的最小值是关键,属于中档题.
| 1-x |
| x |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知A={x|y=x2-1},B={y|y=x2-1},则A∩B( )
| A、∅ | B、A | C、B | D、R |

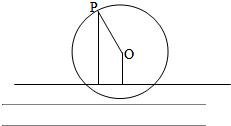 如图是一个半径为3米的水轮,水轮圆心O距离水面2米,已知水轮每分钟转动四圈,水轮上的点P相对于水面的高度y(米)与时间x(秒)满足函数关系y=Asin(ωx+φ)+2(A>0,ω>0,φ∈(-
如图是一个半径为3米的水轮,水轮圆心O距离水面2米,已知水轮每分钟转动四圈,水轮上的点P相对于水面的高度y(米)与时间x(秒)满足函数关系y=Asin(ωx+φ)+2(A>0,ω>0,φ∈(-