题目内容
18.已知($\frac{1}{a}$+ax)5-($\frac{1}{b}$+bx)5的展开式中含x2与x3的项的系数的绝对值之比为1:6,则a2+b2的最小值为( )| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
分析 直接利用($\frac{1}{a}$+ax)5-($\frac{1}{b}$+bx)5的展开式中含x2与x3的项的系数的绝对值之比为1:6,得到ab关系,然后利用基本不等式求解最小值即可.
解答 解:∵($\frac{1}{a}$+ax)5-($\frac{1}{b}$+bx)5的展开式中含x2与x3的项的系数的绝对值之比为1:6,
∴|C52•$\frac{1}{a}$-C52•$\frac{1}{b}$|:|C53•a-C53•b|=1:6,
∴|ab|=6,
∴a2+b2≥2|ab|=12.
故选:C.
点评 本题考查二项式定理的应用,基本不等式的应用,考查计算能力.

练习册系列答案
相关题目
7.已知f(x)=$\left\{\begin{array}{l}{lo{g}_{3}x,x>0}\\{{a}^{x}+b,x≤0}\end{array}\right.$,且f(0)=2,f(-1)=3,则f(f(-3))=( )
| A. | -2 | B. | 2 | C. | 3 | D. | -3 |
8.设集合A={1,2,3},B={2,3},则A∪B=( )
| A. | {2} | B. | {2.5} | C. | {1,2,3} | D. | {1,2,3,5} |
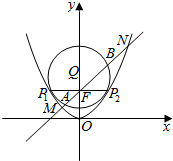 如图,抛物线C:x2=2py(p>0)的焦点为F(0,1),取垂直于y轴的直线与抛物线交于不同的两点P1,P2.过P1,P2作圆心为Q的圆,使抛物线的其余点均在圆外,且P1Q⊥P2Q.
如图,抛物线C:x2=2py(p>0)的焦点为F(0,1),取垂直于y轴的直线与抛物线交于不同的两点P1,P2.过P1,P2作圆心为Q的圆,使抛物线的其余点均在圆外,且P1Q⊥P2Q.