题目内容
【题目】已知常数![]() ,函数
,函数![]() .
.
(1)讨论![]() 在区间
在区间![]() 上的单调性;
上的单调性;
(2)若![]() 存在两个极值点
存在两个极值点![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)详见解析 (2) ![]()
【解析】试题分析:(1)首先对函数![]() 求导并化简得到导函数
求导并化简得到导函数![]() ,导函数的分母恒大于0,分子为含参的二次函数,故讨论分子的符号,确定导函数符号得到原函数的单调性,即分
,导函数的分母恒大于0,分子为含参的二次函数,故讨论分子的符号,确定导函数符号得到原函数的单调性,即分![]() 和
和![]() 得到导函数分子大于0和小于0的解集进而得到函数的单调性.
得到导函数分子大于0和小于0的解集进而得到函数的单调性.
(2)利用第(1)可得到当![]() 时,导数等于0有两个根,根据题意即为两个极值点,首先导函数等于0的两个根必须在原函数
时,导数等于0有两个根,根据题意即为两个极值点,首先导函数等于0的两个根必须在原函数![]() 的可行域内,把
的可行域内,把![]() 关于
关于![]() 的表达式带入
的表达式带入![]() ,得到关于
,得到关于![]() 的不等式,然后利用导函数讨论
的不等式,然后利用导函数讨论![]() 的取值范围使得
的取值范围使得![]() 成立.即可解决该问题.
成立.即可解决该问题.
(1)对函数![]() 求导可得
求导可得
![]()
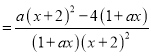
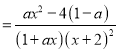 ,因为
,因为![]() ,所以当
,所以当![]() 时,即
时,即![]() 时,
时, ![]() 恒成立,则函数
恒成立,则函数![]() 在
在![]() 单调递增,当
单调递增,当![]() 时,
时, ![]() ,则函数
,则函数![]() 在区间
在区间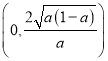 单调递减,在
单调递减,在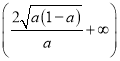 单调递增的.
单调递增的.
(2)解:(1)对函数![]() 求导可得
求导可得![]()
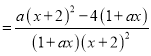
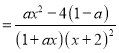 ,因为
,因为![]() ,所以当
,所以当![]() 时,即
时,即![]() 时,
时, ![]() 恒成立,则函数
恒成立,则函数![]() 在
在![]() 单调递增,当
单调递增,当![]() 时,
时, ![]() ,则函数
,则函数![]() 在区间
在区间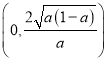 单调递减,在
单调递减,在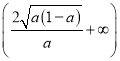 单调递增的.
单调递增的.
(2)函数![]() 的定义域为
的定义域为![]() ,由(1)可得当
,由(1)可得当![]() 时,
时, ![]() ,则
,则![]()
![]()
![]()
![]() ,即
,即![]() ,则
,则![]() 为函数
为函数![]() 的两个极值点,代入
的两个极值点,代入![]() 可得
可得
![]()
![]() =
= ![]()
令![]() ,令
,令![]() ,由
,由![]() 知: 当
知: 当![]() 时,
时, ![]() , 当
, 当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,对
,对![]() 求导可得
求导可得![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减,则
上单调递减,则![]() ,即
,即![]() 不符合题意.
不符合题意.
当![]() 时,
时, ![]() ,对
,对![]() 求导可得
求导可得![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减,则
上单调递减,则![]() ,即
,即![]() 恒成立,
恒成立,
综上![]() 的取值范围为
的取值范围为![]() .
.

【题目】某中学对高二甲、乙两个同类班级进行“加强‘语文阅读理解’训练对提高‘数学应用题’得分率有帮助”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
60分及以下 | 61~70分 | 71~80分 | 81~90分 | 91~100分 | |
甲班(人数) | 3 | 6 | 12 | 15 | 9 |
乙班(人数) | 4 | 7 | 16 | 12 | 6 |
现规定平均成绩在80分以上(不含80分)的为优秀.
(1)由以上统计数据填写![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助;
的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助;
(2)对甲乙两班60分及以下的同学进行定期辅导,一个月后从中抽取3人课堂检测,![]() 表示抽取到的甲班学生人数,求
表示抽取到的甲班学生人数,求![]() 及至少抽到甲班1名同学的概率.
及至少抽到甲班1名同学的概率.
【题目】近年来,随着互联网的发展,诸如“滴滴打车”“神州专车”等网约车服务在我国各城市迅猛发展,为人们出行提供了便利,但也给城市交通管理带来了一些困难.为掌握网约车在![]() 省的发展情况,
省的发展情况,![]() 省某调查机构从该省抽取了5个城市,分别收集和分析了网约车的
省某调查机构从该省抽取了5个城市,分别收集和分析了网约车的![]() ,
,![]() 两项指标数
两项指标数![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
| 2 | 4 | 5 | 6 | 8 |
| 3 | 4 | 4 | 4 | 5 |
经计算得: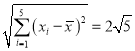 ,
,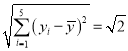 ,
,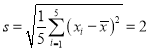 .
.
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并利用
,并利用![]() 说明
说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)建立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标数为7时,
指标数为7时,![]() 指标数的估计值;
指标数的估计值;
(3)若城市的网约车![]() 指标数
指标数![]() 落在区间
落在区间![]() 之外,则认为该城市网约车数量过多,会对城市交通管理带来较大的影响,交通管理部门将介入进行治理,直至
之外,则认为该城市网约车数量过多,会对城市交通管理带来较大的影响,交通管理部门将介入进行治理,直至![]() 指标数
指标数![]() 回落到区间
回落到区间![]() 之内.现已知2018年11月该城市网约车的
之内.现已知2018年11月该城市网约车的![]() 指标数为13,问:该城市的交通管理部门是否要介入进行治理?试说明理由.
指标数为13,问:该城市的交通管理部门是否要介入进行治理?试说明理由.
附:相关公式: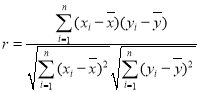 ,
,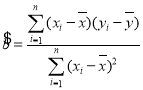 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.


