题目内容
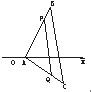如图，已知△ABC的顶点坐标依次为A（1，0），B（5，8），C（7，-4），在边AB上有一点P，其横坐标为4，在AC上求一点Q，使线段PQ把△ABC分成面积相等的两部分．
解：设P分
的比为λ1，由A（1，0）和B（5，8），点P的横坐标为4
∴4=
，解得λ1=3，
即
=3，
=
．
又∵
=•
=
，
∴=
，即
=2．
设λ2=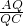
，则λ2=2，
∵A（1，0），C（7，-4），∴xQ=
=5，yQ=
=-
，
∴Q（5，-）．
分析：根据点A、B、P的横坐标求出P分的比值，进而求出的比值，由△APQ和△ABC的面积比和面积公式求出的比值，利用定比分点公式求出点Q的坐标．
点评：本题主要考查了线段定比分点公式的应用，即由点的坐标求出点分向量的比值，再根据面积公式求出对应向量的比值，最后求出分点的坐标．
的比为λ1，由A（1，0）和B（5，8），点P的横坐标为4∴4=
，解得λ1=3，即
=3，=．又∵
=•=，∴
=，即=2．设λ2=
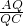，则λ2=2，∵A（1，0），C（7，-4），∴xQ=
=5，yQ==-，∴Q（5，-
）．分析：根据点A、B、P的横坐标求出P分
的比值，进而求出的比值，由△APQ和△ABC的面积比和面积公式求出的比值，利用定比分点公式求出点Q的坐标．点评：本题主要考查了线段定比分点公式的应用，即由点的坐标求出点分向量的比值，再根据面积公式求出对应向量的比值，最后求出分点的坐标．
练习册系列答案
相关题目
如图，已知△ABC的面积为14，D、E分别为边AB、BC上的点，且AD：DB=BE：EC=2：1，AE与CD交于P．设存在λ和μ使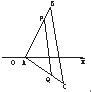
如图，已知△ABC的顶点坐标依次为A（1，0），B（5，8），C（7，-4），在边AB上有一点P，其横坐标为4，在AC上求一点Q，使线段PQ把△ABC分成面积相等的两部分．
如图，已知△ABC的顶点为A（2，4），B（0，-2），C（-2，3），求：
如图，已知△ABC的外角∠EAC的平分线与△ABC的外接圆交于点D，以CD为直径的圆分别交BC，CA于点P、Q，求证：线段PQ平分△ABC的周长．
是边长为2的正三角形，则原△ABC的面积为__________.