题目内容
【题目】在单位圆O:x2+y2=1上任取一点P(x,y),圆O与x轴正向的交点是A,设将OA绕原点O旋转到OP所成的角为θ,记x,y关于θ的表达式分别为x=f(θ),y=g(θ),则下列说法正确的是( )
A.x=f(θ)是偶函数,y=g(θ)是奇函数
B.x=f(θ)在![]() 为增函数,y=g(θ)在
为增函数,y=g(θ)在![]() 为减函数
为减函数
C.f(θ)+g(θ)≥1对于![]() 恒成立
恒成立
D.函数t=2f(θ)+g(2θ)的最大值为![]()
【答案】AC
【解析】
![]() ,由题可知,
,由题可知,![]() ,
,![]() ,根据正弦函数和余弦函数的奇偶性,可判断选项
,根据正弦函数和余弦函数的奇偶性,可判断选项![]() ;
;
![]() ,根据正弦函数和余弦函数的单调性,可判断选项
,根据正弦函数和余弦函数的单调性,可判断选项![]() ;
;
![]() ,先利用辅助角公式可得
,先利用辅助角公式可得![]() ,再结合正弦函数的值域即可得解;
,再结合正弦函数的值域即可得解;
![]() ,
,![]() ,
,![]() ,
,![]() ,先对函数
,先对函数![]() 求导,从而可知函数
求导,从而可知函数![]() 的单调性,进而可得当
的单调性,进而可得当![]() ,
,![]() 时,函数
时,函数![]() 取得最大值,结合正弦的二倍角公式,代入进行运算即可得解.
取得最大值,结合正弦的二倍角公式,代入进行运算即可得解.
解:由题可知,![]() ,
,![]() ,即
,即![]() 正确;
正确;
![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数;
上为减函数;![]() 在
在![]() 上为增函数,即
上为增函数,即![]() 错误;
错误;
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]() ,即
,即![]() 正确;
正确;
函数![]() ,
,![]() 则
则![]() ,
,
令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() ,
,
![]() 函数
函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减,当
上单调递减,当![]() 即
即![]() ,
,![]() 时,函数
时,函数![]() 取得极大值,为
取得极大值,为![]() ,
,
又当![]() 即
即![]() ,
,![]() 时,
时,![]() ,所以函数
,所以函数![]() 的最大值为
的最大值为![]() ,即
,即![]() 错误.
错误.
故选:![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】我国新型冠状病毒肺炎疫情期间,以网络购物和网上服务所代表的新兴消费展现出了强大的生命力,新兴消费将成为我国消费增长的新动能.某市为了了解本地居民在2020年2月至3月两个月网络购物消费情况,在网上随机对1000人做了问卷调查,得如下频数分布表:
网购消费情况(元) |
|
|
|
|
|
频数 | 300 | 400 | 180 | 60 | 60 |
(1)作出这些数据的频率分布直方图,并估计本市居民此期间网络购物的消费平均值;
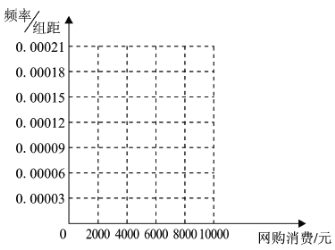
(2)在调查问卷中有一项是填写本人年龄,为研究网购金额和网购人年龄的关系,以网购金额是否超过4000元为标准进行分层抽样,从上述1000人中抽取200人,得到如下列联表,请将表补充完整并根据列联表判断,在此期间是否有95%的把握认为网购金额与网购人年龄有关.
网购不超过4000元 | 网购超过4000元 | 总计 | |
40岁以上 | 75 | 100 | |
40岁以下(含40岁) | |||
总计 | 200 |
参考公式和数据:![]() .(其中
.(其中![]() 为样本容量)
为样本容量)
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |