题目内容
函数y=2sin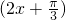
（-
＜x＜）的值域________．
（0，2]
分析：将2x+
看成整体，转化成基本的三角函数y=sinx在给定范围内的值域问题．
解答：∵-＜x＜，
∴0＜2x+＜
，
根据正弦函数的性质，则0＜sin（2x+）≤1，
∴0＜2sin（2x+）≤2
∴函数y=2sin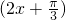 （-＜x＜）的值域 （0，2]．
故答案为：（0，2]．
点评：本题属于求三角函数值域的基本问题，数形结合在三角函数中是常用的方法．
分析：将2x+
看成整体，转化成基本的三角函数y=sinx在给定范围内的值域问题．解答：∵-
＜x＜，∴0＜2x+
＜，根据正弦函数的性质，则0＜sin（2x+
）≤1，∴0＜2sin（2x+
）≤2∴函数y=2sin
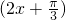（-＜x＜）的值域 （0，2]．故答案为：（0，2]．
点评：本题属于求三角函数值域的基本问题，数形结合在三角函数中是常用的方法．
练习册系列答案
相关题目
如图所示，点P是函数y=2sin（ωx+φ）（x∈R，ω＞0）图象的最高点，M、N是图象与x轴的交点，若函数y=2sin(2x-
)的图象（ ）
| π |
| 6 |
| A、关于原点成中心对称 | ||
| B、关于y轴成轴对称 | ||
C、关于(
| ||
D、关于直线x=
|