题目内容
先后抛掷两枚均匀的正方体骰子(他们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为x、y,则log2xy=1的概率为( )
A.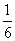 B.
B.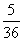
C. D.
D.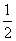
C
[解析] 先后抛掷两枚骰子,向上点数共有6×6=36种不同结果,其中满足log2xy=1,
即y=2x的情况如下:
x=1时,y=2;x=2时,y=4;x=3时,y=6,共3种.
∴所求概率为P= =
= .
.
[点评] 注意细微差别,若把题目中的条件log2xy=1改为log2xy>1,则所求概率为( )
此时答案为A
这是因为抛掷两枚骰子共有62=36种不同结果,
∵log2xy>1,∴y>2x.
当x=1时,y有4种取法;当x=2时,y有2种取法;当x=3时,没有y满足,
∴满足y>2x的取法共有4+2=6种,
故所求概率P= =
=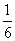 .
.
若改为logx2y<1呢?

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
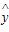 =
=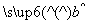 x+
x+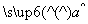 ,则“(x0,y0)满足线性回归方程
,则“(x0,y0)满足线性回归方程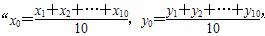 的( )
的( )
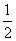 ,构造数列{an},使得an=
,构造数列{an},使得an= ,
, B.
B.
 D.
D.