题目内容
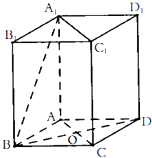 四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,且ABCD是菱形,AC、BD相交于点O,AB=BC=2,AA1=4,∠ABC=60°.
四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,且ABCD是菱形,AC、BD相交于点O,AB=BC=2,AA1=4,∠ABC=60°.(1)求证:BD⊥平面ACC1A1;
(2)求A1B与平面ACC1A1所成角的正弦值.
分析:(1)先利用直线与平面垂直的性质证明出AA1⊥BD,在由平行四边形ABCD中的已知条件推导出AC⊥BD,由此能够证明BD⊥平面ACC1A1.
(2)连结A1O,由(1)知A1B在平面ACC1A1内的射影是A1O,从而得到A1B与平面ACC1A1所成的角是∠BA1O,由此能求出A1B与平面ACC1A1所成角的正弦值.
(2)连结A1O,由(1)知A1B在平面ACC1A1内的射影是A1O,从而得到A1B与平面ACC1A1所成的角是∠BA1O,由此能求出A1B与平面ACC1A1所成角的正弦值.
解答:(1)证明:在四棱柱ABCD-A1B1C1D1中,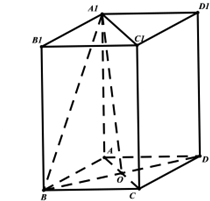
∵AA1⊥平面ABCD,
∴AA1⊥BD,
平行四边形ABCD中,
∵AB=BC,∴AC⊥BD,
∵AA1∩AC=A,∴BD⊥平面ACC1A1.
(2)连结A1O,由(1)知A1B在平面ACC1A1内的射影是A1O,
则A1B与平面ACC1A1所成的角是∠BA1O,
∵在平行四边形ABCD中,AB=BC=2,∠ABC=60°,
∴BO=
,
∵AA1=4,AB=2,∴A1B=2
,
∴在Rt△A1OB中,sin∠BA1O=
=
=
.
∴A1B与平面ACC1A1所成角的正弦值是
.

∵AA1⊥平面ABCD,
∴AA1⊥BD,
平行四边形ABCD中,
∵AB=BC,∴AC⊥BD,
∵AA1∩AC=A,∴BD⊥平面ACC1A1.
(2)连结A1O,由(1)知A1B在平面ACC1A1内的射影是A1O,
则A1B与平面ACC1A1所成的角是∠BA1O,
∵在平行四边形ABCD中,AB=BC=2,∠ABC=60°,
∴BO=
| 3 |
∵AA1=4,AB=2,∴A1B=2
| 5 |
∴在Rt△A1OB中,sin∠BA1O=
| BO |
| A1B |
| ||
2
|
| ||
| 10 |
∴A1B与平面ACC1A1所成角的正弦值是
| ||
| 10 |
点评:本题考查直线与平面垂直的证明,考查直线与平面所成角的正弦值,解题时要注意空间思维能力的培养.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=2
如图,在直四棱柱ABCD-A1B1C1D1中,AB=AD=2,DC=2 如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.
如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.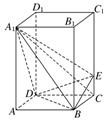 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上,且CE=λCC1.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上,且CE=λCC1.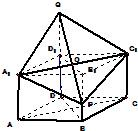 如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为2、∠ADC=120°的菱形,Q是侧棱DD1(DD1>
如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为2、∠ADC=120°的菱形,Q是侧棱DD1(DD1>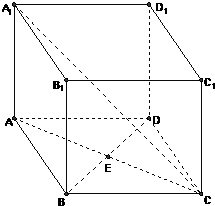 如图,直四棱柱ABCD-A1B1C1D1中,AB=AD=2,CB=CD=2
如图,直四棱柱ABCD-A1B1C1D1中,AB=AD=2,CB=CD=2