题目内容
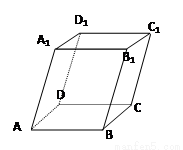
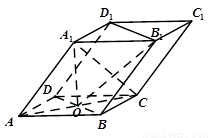
 如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.
如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.①求证四棱锥A1-ABCD为正四棱锥;
②求侧面A1ABB1与截面B1BDD1的锐二面角大小.
分析:(1)欲证四棱锥A1-ABCD是正四棱锥,设A1在底面ABCD的射影为O,即证O是底面正方形ABCD的中心即可,而O是Rt△ABD的外心,因为Rt△ABD的外心是斜边BD的中点,该中点就是正方形的中心;
(2)取AA1的中点M,根据定义可知∠MBD是所求二面角的平面角,然后在三角形MBD中求解此角即可.
(2)取AA1的中点M,根据定义可知∠MBD是所求二面角的平面角,然后在三角形MBD中求解此角即可.
解答:解:(1)由AA1=AD=AB,及∠A1AD=∠A1AB=60°?△A1AD、△AA1B都是正三角形,
从而AA1=A1D=A1B,设A1在底面ABCD的射影为O,则由斜线长相等推出射影长也相等,
所以O是Rt△ABD的外心,因为Rt△ABD的外心是斜边BD的中点,
所以O是底面正方形ABCD的中心.所以四棱锥A1-ABCD是正四棱锥.
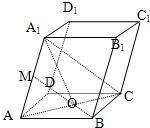
(2)由DB⊥平面AA1O?截面BB1D1D⊥平面AA1O?点O与侧棱AA1的距离d等于AA1和截面BB1D1D之间的距离.
取AA1的中点M,则OM∥A1C,且OM⊥AA1,OM=
A1C=
a,
∴所求距离为
a.注意到所求二面角的棱是B1B,
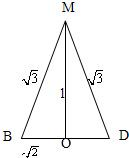
由M是AA1的中点?MB⊥AA1,B1B∥AA1?MB⊥B1B,又DB⊥AA1,AA1∥B1B?DB⊥B1B,
∴∠MBD是所求二面角的平面角.不妨设AB=a=2,则BD=2
,MB=MD=
,
∴tan∠MBD=
.
∴侧面A1ABB1与截面B1BDD1的夹角为arctan
.
从而AA1=A1D=A1B,设A1在底面ABCD的射影为O,则由斜线长相等推出射影长也相等,
所以O是Rt△ABD的外心,因为Rt△ABD的外心是斜边BD的中点,
所以O是底面正方形ABCD的中心.所以四棱锥A1-ABCD是正四棱锥.

(2)由DB⊥平面AA1O?截面BB1D1D⊥平面AA1O?点O与侧棱AA1的距离d等于AA1和截面BB1D1D之间的距离.
取AA1的中点M,则OM∥A1C,且OM⊥AA1,OM=
| 1 |
| 2 |
| 1 |
| 2 |
∴所求距离为
| 1 |
| 2 |
由M是AA1的中点?MB⊥AA1,B1B∥AA1?MB⊥B1B,又DB⊥AA1,AA1∥B1B?DB⊥B1B,
∴∠MBD是所求二面角的平面角.不妨设AB=a=2,则BD=2
| 2 |
| 3 |
∴tan∠MBD=
| ||
| 2 |

∴侧面A1ABB1与截面B1BDD1的夹角为arctan
| ||
| 2 |
点评:本小题主要考查二面角及其度量,以及棱锥的结构特征等知识,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
相关题目
 如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.
如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.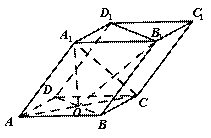
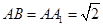 .
. 
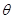 的大小.
的大小.